Is Zero Considered a Rational Number? A Simple Explanation That Sticks
Ask any student wrestling with fractions: is zero a rational number? The clean answer in mathematics is yes. A rational number is any value that can be written as a fraction p/q where p and q are integers, and the denominator q is not zero. Since 0 can be expressed as 0/1, 0/7, or more generally 0/n for any nonzero integer n, it fits neatly. But the story gets richer when the lens widens to number theory, limits, and how learners internalize math concepts. To keep things relatable, meet Maya, a high school coder who tutors younger kids; she loves a simple explanation backed by crisp examples and pattern-spotting.
Maya starts with a quick checklist. If a number has a valid fraction form with integer numerator and nonzero denominator, it’s rational. Zero passes because its numerator can be 0 while its denominator can be any nonzero integer. Division by zero is off-limits, but that rule concerns the denominator, not the number zero itself. In class, this distinction prevents the classic mix-up: 0/5 is valid (and equals 0), whereas 5/0 is undefined. That one line saves hours of confusion.
For learners who enjoy context, zero also sits inside other sets. It’s an integer (…−2, −1, 0, 1, 2…), a whole number (0, 1, 2, 3, …), and a real number (part of the full continuum including both rational and irrational values). However, many textbooks define natural numbers as starting at 1, which excludes 0; some computer science contexts include 0 as natural. Knowing which convention a course uses avoids needless debates.
In 2025 classrooms, teachers increasingly use AI and explainers to make these distinctions memorable. Tools that help organize examples—like project boards and content planners—mirror the neatness of fraction definitions. For a glimpse at how structured thinking tools are reshaping learning workflows, resources on automation with APIs or a snapshot of education-centric tech trends illustrate how clarity scales. Even quirky explorations—say, what a billion seconds feels like—can contextualize large and small numbers that appear across lessons on fractions and place value.
- ✅ Zero is rational because it equals 0/n with n ≠ 0.
- 🚫 Division by zero (like 5/0) is undefined, unrelated to zero’s rationality.
- 🧩 Zero belongs to multiple sets: integer, whole, and real numbers.
- 🧠 Conventions vary for natural numbers; check your course definition.
- 🎯 Use the fraction test: integer numerator and nonzero denominator.
| Number 🔢 | Rational? ✅/❌ | Reason 💡 |
|---|---|---|
| 0 | ✅ | Can be written as 0/1, 0/5, … with integer parts and nonzero denominator. |
| 5 | ✅ | Equals 5/1 (integer fraction form). |
| 1/3 | ✅ | Integer numerator and denominator; decimal is repeating. |
| π | ❌ | Cannot be expressed as a ratio of integers; decimal is nonrepeating. |
| √2 | ❌ | Proven irrational; no integer fraction equals √2. |
Key insight to carry forward: the fraction definition alone settles zero’s status—no drama, just structure.

Pivot from Fraction Form to Real-Life Uses of Zero
Before rolling into properties, Maya asks a practical question: where does zero show up outside of worksheets? In budgets, a zero line means no spend; in code, 0 flags false or empty; in data dashboards, 0 marks baseline. The same clarity required to treat 0 as rational helps teams label, compare, and compute without ambiguities. For developers experimenting with time utilities, understanding zero as a starting offset aligns with reliable tooling like accurate time retrieval in Swift for interval arithmetic.
Why 0 Fits the Rational Number Definition: Fractions, Decimals, and Algebra
Beyond the formal definition, the versatility of zero as a rational number emerges in multiple representations. In any fraction p/q, if p = 0 and q ≠ 0, the value is 0. That’s why 0/1 = 0/9 = 0/−13 = 0. Switching signs or changing the denominator doesn’t change the value because multiplying or dividing zero by any nonzero integer still yields zero. This makes 0 the most stable fraction value under equivalent transformations.
Decimals tell the same story. A rational number has a terminating or repeating decimal expansion. Zero’s decimal is 0.0, 0.000…, or any equivalent string with finitely many or infinitely many zeros afterward—every option is terminating in effect. If a student sees 0.000, the key is that there are no nonzero digits after the decimal; thus, it’s rational and equals 0.
Algebra deepens the intuition. Zero is the additive identity: for any number a, a + 0 = a. This identity pairs nicely with rational arithmetic rules. For example, adding 0 to a rational number p/q keeps p/q rational. Multiplying any rational by 0 yields 0, which is again rational. The closure properties of rational numbers and the special role of 0 reinforce each other: nothing breaks when zero joins the party.
Maya demonstrates with a classroom routine that learners can copy into notes or flashcards. The routine avoids shortcuts and surfaces the rules that actually matter.
- 🧪 Fraction test: write the number as p/q with integers p, q and q ≠ 0 → rational.
- 🔁 Decimal test: terminating or repeating → rational (0’s decimal is all zeros).
- ➕ Identity check: adding 0 changes nothing; multiplication by 0 returns 0.
- 🧭 Sign sanity: 0/−7 = 0/7 = 0; the sign in the denominator doesn’t matter.
- ⚠️ Red flag: a denominator of 0 makes the expression undefined, not “irrational.”
| Representation 🧮 | Example | Rational? 🔍 | Reasoning 🧠 |
|---|---|---|---|
| Fraction | 0/19 | ✅ | Integer numerator and nonzero denominator → value is 0. |
| Decimal | 0.000… | ✅ | Terminating (or effectively terminating) decimal form. |
| Integer form | 0 | ✅ | Every integer is rational (n = n/1). |
| Mixed number | 0 0/5 | ✅ | Equivalent to 0; the fractional part vanishes. |
| Scientific notation | 0.0 × 10³ | ✅ | Still 0; notation doesn’t affect rationality. |
For learners who enjoy crossovers with tech, AI-powered draft coaches can help explainers stay consistent; see how a writing coach for clarity or curated libraries for structured outputs mirror the reliability of fraction rules. And if progress needs tracking over weeks, utilities like calendar-based counters are handy companions.
Bottom line: whether written as a fraction, a decimal, or an integer, zero remains rational—and that consistency is exactly what makes it so useful.
Common Misconceptions About Zero: Division, Limits, and “Tricky” Cases
The loudest confusion around zero stems from mixing separate rules. The classic pitfall is conflating “division by zero is undefined” with “zero is not rational.” They have nothing to do with each other. In a fraction p/q, the only forbidden move is q = 0. Setting p = 0 is allowed and harmless. Maya uses a quick analogy: a denominator of zero is like asking for seats on a flight that doesn’t exist—no boarding pass will fix it. But having a numerator of zero just means zero passengers showed up; the flight still exists.
Limits create the next knot. Consider lim (x→0) 1/x. Approaching from the positive side races to +∞; from the negative side, it plunges to −∞. This tells us something about behavior near zero, not about the value of zero or its rationality. Similarly, “indeterminate forms” like 0/0 appear in calculus when evaluating limits, but the expression 0/0 is undefined as a number. None of these analytic ideas revoke zero’s membership in the rational set.
Other tricky spots surface in combinatorics and algebra. The factorial 0! equals 1 by definition (consistent with recursion and empty product logic), which is rational. Exponentiation can also look strange: 0^0 is left undefined in many contexts because competing extensions would contradict desirable properties; in discrete math, it’s sometimes taken as 1 to simplify formulas. Regardless of these edge rules, the value 0 remains rational.
- 🧯 Myth: “Division by zero proves 0 isn’t rational.” Reality: only denominators can’t be 0; numerators can.
- 📉 Myth: “Limits at 0 define what zero ‘is.’” Reality: limits describe nearby behavior, not zero’s identity.
- 🧩 Fact: 0! = 1 → rational; 0^0 is context-sensitive but doesn’t affect zero’s rationality.
- 🔄 Fact: Repeating decimals indicate rationality; zero’s decimal is a trivial repeat of 0s.
- 🧭 Pro tip: Keep arithmetic rules, limit laws, and set definitions in separate mental drawers.
| Expression/Idea 🧠 | Status | Impact on Zero’s Rationality 🎯 | Student Tip ✍️ |
|---|---|---|---|
| 5/0 | Undefined ❌ | None; unrelated to whether 0 is rational. | Denominator can’t be 0. Full stop. |
| 0/5 | Valid ✅ | Confirms 0 as a rational number. | Any nonzero denominator works. |
| lim (x→0) 1/x | No finite limit | Doesn’t classify 0; it’s about behavior near 0. | Separate calculus from arithmetic. |
| 0! | Equals 1 | Rational (1/1) ✅ | Empty product convention. |
| 0^0 | Context-dependent | No change to zero’s status | Follow your course rules. |
When mental models need sharpening, well-structured workflows help. Articles on improving evaluation discipline, such as measuring what matters in 2025 classrooms, or tackling context shifts, as with managing context windows, show how careful definitions prevent category errors. Clear categories are exactly what keep zero rational and division by zero off-limits—two truths living happily side by side.

Bridge to History and Axioms
Students often ask: if the rules are so tidy, why did humanity struggle to adopt zero? That’s the perfect segue to the story of placeholders, merchants, and the axioms that cemented today’s definitions.
From Ancient Placeholders to Modern Axioms: How Zero Earned Its Seat
Zero’s path from “nothing” to a full-fledged number was anything but immediate. Babylonian scribes used a placeholder symbol to keep place value straight, but the concept of zero as a standalone number took root in India, with mathematicians like Brahmagupta articulating arithmetic with zero around the 7th century. Trade and scholarship carried these ideas across the Islamic world and into Europe, where resistance gradually softened as positional notation proved itself indispensable in commerce and astronomy. The rise of algebra, and later calculus, locked in zero’s centrality.
Modern axiomatic approaches make the classification airtight. Starting with structures like the Peano axioms for natural numbers, mathematicians construct integers from equivalence classes of pairs of naturals, and rationals from equivalence classes of integer pairs (p, q) with q ≠ 0. In that construction, the class [(0, 1)] represents the rational number 0—clean and unambiguous. That’s why textbooks state without hesitation that zero is rational. The only wiggle room lies in whether “natural numbers” include zero; either choice is consistent, but teachers must state their convention.
Maya uses a short timeline to help learners anchor the evolution. It makes the present-day definition feel like the end of a long engineering project: the pieces click because they were designed to.
- 📜 Placeholders in ancient Babylon set the stage for positional notation.
- 🧮 Indian mathematicians formalized arithmetic with zero and negative numbers.
- 🌍 Knowledge transfer through trade solidified 0 in global mathematics.
- 🏛️ Axiomatic set-ups derived rational numbers from integers with q ≠ 0.
- 🔧 Computing and data science standardized zero’s role in indexing and logic.
| Era ⏳ | Milestone | Impact on Rationality of 0 🎯 | Memory Hook 📌 |
|---|---|---|---|
| Ancient | Placeholder emerges | Prepares positional thinking but not yet a number | “Empty seat” in numeral line |
| Classical India | 0 as a number with operations | Arithmetic rules stabilize | 0 × a = 0, a + 0 = a |
| Medieval transmission | Trade and scholarship spread place value | Notation standardizes | Merchants need zeros |
| Modern axioms | Build ℚ from integers via pairs (p, q) | [(0, 1)] is rational 0 ✅ | q ≠ 0 is the only constraint |
Educators today often blend historical context with digital tools to sharpen retention. Classroom blogs that unpack sensitive tech stories—like legal debates involving AI—model how precise definitions matter. Similarly, pieces comparing assistants, such as Copilot vs. ChatGPT, echo the idea that consistent rules lead to trustworthy outcomes. Even discussions about data handling and file analysis reinforce a lesson: clean inputs and clear constraints—like q ≠ 0—keep systems stable.
Takeaway for learners: zero didn’t just appear; it was engineered into the number system, and its rational status is baked in by construction.
Hands-On Reasoning: Classifying Numbers Quickly (With Zero as the Anchor)
With the big picture set, Maya runs a “90-second sorter” for problem sets. The idea is to classify any input rapidly by checking fraction form, decimal behavior, and set inclusion—using zero as the anchor case. The goal is speed without sloppiness. Learners can even build a mini cheat-sheet for test margins.
Start with the fraction test. Can it be p/q with integers p, q and q ≠ 0? If yes, it’s rational. If the decimal form terminates or repeats (like 0.125 or 0.333…), it’s rational. If it neither terminates nor repeats (like π or √2 as decimals), it’s irrational. For integers, remember that n = n/1 makes every integer rational; thus 0 is rational because 0 = 0/1. These checks apply uniformly across exercises.
- 🧩 Step 1: Try p/q with integer parts; reject q = 0 immediately.
- 🔎 Step 2: Inspect decimals: terminating or repeating → rational.
- 🧱 Step 3: Integers auto-qualify (n = n/1), including 0.
- 🛑 Step 4: If neither holds and decimals never repeat → irrational.
- 🗂️ Step 5: Note set membership (whole, integer, real) for full credit.
| Value 🔢 | Fraction Form | Rational? ✅/❌ | Set Tags 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | Integer, Whole, Real |
| −3/4 | −3/4 | ✅ | Rational, Real |
| 0.125 | 1/8 | ✅ | Rational, Real |
| 0.333… | 1/3 | ✅ | Rational, Real |
| √2 | — | ❌ | Irrational, Real |
| π | — | ❌ | Irrational, Real |
Want audiovisual reinforcement? A quick explainer video can lock in the rational vs. irrational boundary while keeping zero at center stage. For teachers building playlists, structured queries can help surface concise clips.
Tech-minded learners often prototype note systems and pipelines; if that’s your style, modular workflows like virtualized media servers can host study resources, and task automation via API tools can auto-generate practice decks focusing on tricky boundary cases like 0, 0/0 (undefined), and 1/0 (undefined). A clean pipeline reinforces a clean definition.
Final thought for this section: consistency wins. Zero behaves the same way across representations, making it the perfect anchor for the sorter.
Edge Applications: Place Value, Data Systems, and Classroom Storylines Where Zero Matters
Zero’s rationality isn’t just a proof; it underpins how information systems and curricula behave. In base-ten place value, a 0 digit signals “none of this place,” which keeps magnitude correct: 101 differs from 11 because the middle 0 preserves the tens place as empty. In spreadsheets and code, a zero often indicates “no items,” “no error,” or baseline—making calculations deterministic. A disorganized treatment of 0 would inject chaos into dashboards, time math, and algorithms.
Consider data classification tasks: if a column should store rational numbers only, zero must be admitted, or else legitimate measurements at baseline would be rejected. Maya designs a small “data hygiene” demo: feed a parser a mix of integers, simple fractions, repeating decimals, and known irrationals; the validator accepts anything convertible to p/q with q ≠ 0. The demo logs 0 as valid across integer and fraction paths. From there, students write unit tests to confirm closure under addition and multiplication with zero.
- 🧮 Place value: 0 keeps digits aligned, preventing magnitude mistakes.
- 🧰 Data integrity: zero must validate in rational-only fields.
- 🧷 Error handling: 1/0 errors are caught at parse-time, not runtime.
- 🧪 Testing: include 0 in all closure property tests for rationals.
- 📚 Storyline: Maya labels 0 as “the anchor” in rubrics and project docs.
| Scenario 🗂️ | Zero’s Role | Why Rationality Helps 🎓 | Classroom Cue 🛎️ |
|---|---|---|---|
| Place value | Holds empty positions | Consistent magnitude interpretation | “0 keeps the seat warm” 😊 |
| Validation | Accepted as 0/1 | Clean input constraints | Test 0, 1/0, 0/0 separately |
| Computation | Additive identity | Simplifies proofs and code | Use 0 in unit tests |
| Teaching | Anchor case | Reduces misconception spread | Start examples with 0 |
Curiosity break: communication around math benefits from precise language and context. Even outside math, clarity matters—whether parsing emoji meanings for tone in student forums, evaluating school safety tech, or spotting news narratives. The lesson transfers: definitions, constraints, and examples prevent confusion. By the same token, a harmless rabbit hole like symbol interpretation reminds learners how quickly meaning can drift without shared rules—exactly why the rational definition keeps zero grounded.
Closing insight for this segment: zero’s rationality is more than a label; it’s a guarantee that systems—from arithmetic to analytics—stay predictable.
Extra Practice with Maya’s Mini-Set
Maya’s students classify these in under a minute: 0, −7, 2/9, 0/3, 3/0, 0.1010010001…, and √9. The wins: 0 (rational), −7 (rational), 2/9 (rational), 0/3 (rational), 3/0 (undefined), 0.1010010001… (nonrepeating, nonterminating → likely irrational), √9 (equals 3 → rational). The pattern-spotting skill transfers across units and tests.
Is zero considered a rational number?
Yes. By definition, a rational number is any value expressible as p/q with integers p and q and q ≠ 0. Zero fits because 0 = 0/1, 0/5, or 0/n for any nonzero integer n.
Does division by zero make zero non-rational?
No. Division by zero is a rule about denominators, not about the number zero. 5/0 and 0/0 are undefined expressions, but 0 itself remains a valid rational number.
Is zero an integer, whole, or natural number?
Zero is an integer and a whole number. Whether it is a natural number depends on convention: many courses start naturals at 1, while some contexts include 0.
Can zero be written as a decimal and still be rational?
Yes. Zero’s decimal form is 0.0 (or 0.000…), which is terminating. Terminating and repeating decimals are rational by definition.
How does zero’s role help in algebra?
Zero is the additive identity: a + 0 = a. It keeps equations balanced and simplifies proofs. Multiplying any rational number by 0 gives 0, which is rational.
Jordan has a knack for turning dense whitepapers into compelling stories. Whether he’s testing a new OpenAI release or interviewing industry insiders, his energy jumps off the page—and makes complex tech feel fresh and relevant.
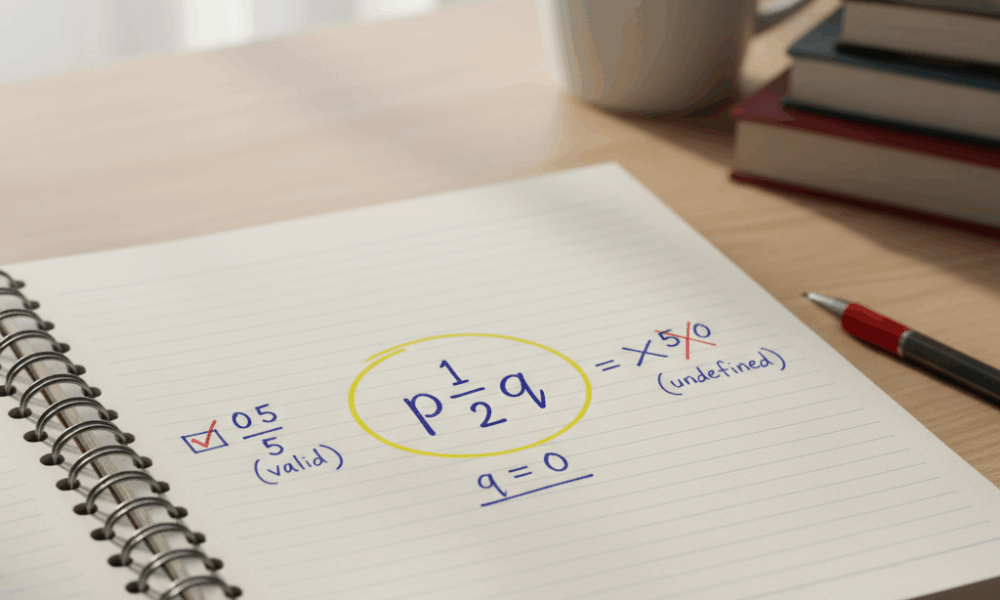


Comments are closed