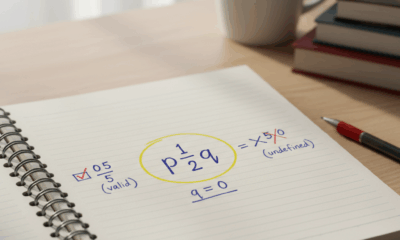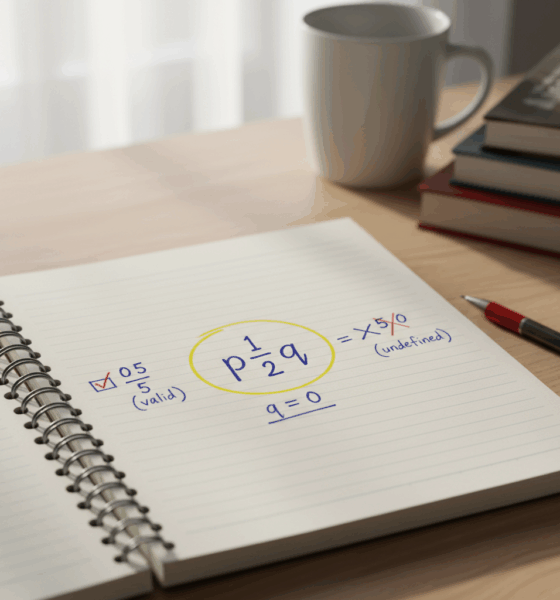
Tech
wird Null als rationale Zahl betrachtet? Einfach erklärt
Ist Null eine rationale Zahl? Eine einfache Erklärung, die haften bleibt
Fragen Sie jeden Schüler, der mit Brüchen kämpft: Ist Null eine rationale Zahl? Die klare Antwort in der Mathematik lautet ja. Eine rationale Zahl ist jeder Wert, der als Bruch p/q geschrieben werden kann, wobei p und q ganze Zahlen sind und der Nenner q nicht null ist. Da 0 als 0/1, 0/7 oder allgemein als 0/n für jede von null verschiedene ganze Zahl n dargestellt werden kann, passt sie perfekt hinein. Aber die Geschichte wird reichhaltiger, wenn der Blick auf Zahlentheorie, Grenzwerte und darauf weitet, wie Lernende Mathe-Konzepte verinnerlichen. Um es nachvollziehbar zu halten, lernen wir Maya kennen, eine Programmiererin in der Oberstufe, die jüngere Kinder unterrichtet; sie mag eine einfache Erklärung, die durch klare Beispiele und Mustererkennung unterstützt wird.
Maya beginnt mit einer kurzen Checkliste. Wenn eine Zahl eine gültige Bruchform mit ganzzahligem Zähler und von null verschiedenenm Nenner hat, ist sie rational. Null besteht, weil ihr Zähler 0 sein kann, während ihr Nenner eine beliebige von null verschiedene ganze Zahl ist. Division durch null ist tabu, aber diese Regel betrifft den Nenner, nicht die Zahl Null selbst. Im Unterricht verhindert diese Unterscheidung das klassische Missverständnis: 0/5 ist gültig (und gleich 0), während 5/0 undefiniert ist. Diese eine Zeile spart stundenlange Verwirrung.
Für Lernende, die Kontext mögen, gehört Null auch zu anderen Mengen. Sie ist eine ganze Zahl (…−2, −1, 0, 1, 2…), eine volle Zahl (0, 1, 2, 3, …) und eine reelle Zahl (Teil des gesamten Kontinuums, das rationale und irrationale Werte einschließt). Allerdings definieren viele Lehrbücher natürliche Zahlen als beginnend bei 1, was 0 ausschließt; einige Informatikkontexte schließen 0 als natürlich ein. Zu wissen, welche Konvention ein Kurs verwendet, vermeidet unnötige Debatten.
Im Unterrichtsjahr 2025 nutzen Lehrkräfte zunehmend KI und Erklärhilfen, um diese Unterscheidungen einprägsam zu machen. Werkzeuge, die beim Organisieren von Beispielen helfen – wie Projektboards und Inhaltsplaner – spiegeln die Klarheit der Bruchdefinitionen wider. Ein Blick darauf, wie strukturierte Denkwerkzeuge Lernabläufe verändern, findet sich in Ressourcen zu Automatisierung mit APIs oder in einer Übersicht zu bildungsspezifischen Technologietrends, die veranschaulichen, wie sich Klarheit skalieren lässt. Selbst skurrile Erkundungen – etwa wie sich eine Milliarde Sekunden anfühlen – können große und kleine Zahlen kontextualisieren, die in Lektionen zu Brüchen und Stellenwert auftauchen.
- ✅ Null ist rational, weil sie gleich 0/n ist mit n ≠ 0.
- 🚫 Division durch Null (wie 5/0) ist undefiniert, hat nichts mit der Rationalität von Null zu tun.
- 🧩 Null gehört zu mehreren Mengen: ganzen Zahlen, vollen Zahlen und reellen Zahlen.
- 🧠 Konventionen variieren bei den natürlichen Zahlen; überprüfen Sie Ihre Kursdefinition.
- 🎯 Verwenden Sie den Bruchtest: ganzzahliger Zähler und von Null verschiedener Nenner.
| Zahl 🔢 | Rational? ✅/❌ | Begründung 💡 |
|---|---|---|
| 0 | ✅ | Kann als 0/1, 0/5, … mit ganzzahligen Teilen und von Null verschiedenem Nenner geschrieben werden. |
| 5 | ✅ | Gleich 5/1 (ganzzahliger Bruch). |
| 1/3 | ✅ | Ganzzahliger Zähler und Nenner; Dezimalbruch ist periodisch. |
| π | ❌ | Kann nicht als Verhältnis ganzer Zahlen dargestellt werden; Dezimalbruch ist nicht periodisch. |
| √2 | ❌ | Bewiesen irrational; kein ganzzahliger Bruch entspricht √2. |
Wichtig zu merken: Die Bruchdefinition allein klärt den Status von Null – kein Drama, nur Struktur.

Vom Bruch zur Praxis: Wo Null im echten Leben auftaucht
Bevor sie auf Eigenschaften eingeht, stellt Maya eine praktische Frage: Wo taucht Null außerhalb von Arbeitsblättern auf? In Budgets bedeutet eine Null-Zeile keine Ausgabe; im Code signalisiert 0 falsch oder leer; in Daten-Dashboards markiert 0 die Basislinie. Dieselbe Klarheit, um 0 als rational zu betrachten, hilft Teams dabei, zu beschriften, zu vergleichen und ohne Unklarheiten zu rechnen. Für Entwickler, die mit Zeit-Utilities experimentieren, stimmt das Verständnis von Null als Ausgangssprungpunkt mit zuverlässigen Werkzeugen wie genauer Zeitabfrage in Swift für Intervallarithmetik überein.
Warum 0 zur Definition rationaler Zahlen passt: Brüche, Dezimalzahlen und Algebra
Über die formale Definition hinaus zeigt sich die Vielseitigkeit von Null als rationale Zahl in mehreren Darstellungen. In jedem Bruch p/q gilt: Wenn p = 0 und q ≠ 0, ist der Wert 0. Deshalb gilt 0/1 = 0/9 = 0/−13 = 0. Das Wechseln von Vorzeichen oder Ändern des Nenners ändert den Wert nicht, weil Mal- oder Teilen von Null mit jeder von null verschiedenen ganzen Zahl ebenfalls Null ergibt. Das macht 0 zum stabilsten Bruchwert bei äquivalenten Umformungen.
Dezimalzahlen erzählen dieselbe Geschichte. Eine rationale Zahl hat eine endliche oder periodische Dezimaldarstellung. Nulls Dezimaldarstellung ist 0,0, 0,000… oder jede äquivalente Folge mit endlich oder unendlich vielen Nullen danach – jede Option ist effektiv terminierend. Wenn ein Schüler 0,000 sieht, ist der Schlüssel, dass keine nicht-null Ziffern nach dem Komma folgen; somit ist sie rational und gleich 0.
Algebra vertieft die Intuition. Null ist das additive Identitätselement: Für jede Zahl a gilt a + 0 = a. Diese Identität harmoniert gut mit den Regeln der rationalen Arithmetik. Zum Beispiel bleibt p/q rational, wenn man 0 addiert. Jede rationale Zahl mal 0 ergibt 0, was ebenfalls rational ist. Die Abgeschlossenheit der rationalen Zahlen und die besondere Rolle von 0 stärken sich gegenseitig: Nichts geht kaputt, wenn Null dazukommt.
Maya zeigt eine Routine, die Lernende ins Notizbuch oder auf Karteikarten übernehmen können. Diese Routine vermeidet Abkürzungen und macht die wirklich wichtigen Regeln sichtbar.
- 🧪 Bruchtest: Schreibe die Zahl als p/q mit ganzen Zahlen p, q und q ≠ 0 → rational.
- 🔁 Dezimaltest: endend oder periodisch → rational (Nulls Dezimalzahl besteht nur aus Nullen).
- ➕ Identitätscheck: 0 addieren ändert nichts; multiplizieren mit 0 ergibt 0.
- 🧭 Vorzeichencheck: 0/−7 = 0/7 = 0; Vorzeichen im Nenner spielt keine Rolle.
- ⚠️ Warnung: Nenner 0 macht Ausdruck undefiniert, nicht „irrational“.
| Darstellung 🧮 | Beispiel | Rational? 🔍 | Begründung 🧠 |
|---|---|---|---|
| Bruch | 0/19 | ✅ | Ganzzahliger Zähler und von null verschiedener Nenner → Wert ist 0. |
| Dezimal | 0,000… | ✅ | Terminierende (bzw. effektiv terminierende) Dezimalform. |
| Ganze Zahl | 0 | ✅ | Jede ganze Zahl ist rational (n = n/1). |
| Gemischte Zahl | 0 0/5 | ✅ | Dem Wert 0 entsprechend; der Bruchanteil fällt weg. |
| Wissenschaftliche Schreibweise | 0,0 × 10³ | ✅ | Immer noch 0; die Notation beeinflusst die Rationalität nicht. |
Für technisch interessierte Lernende können KI-gestützte Entwurfscoaches helfen, Erklärungen konsistent zu halten; sehen Sie, wie ein Schreibcoach für Klarheit oder kuratierte Bibliotheken für strukturierte Ausgaben die Verlässlichkeit der Bruchregeln widerspiegeln. Und falls Fortschritte über Wochen verfolgt werden müssen, sind Werkzeuge wie kalenderbasierte Zähler nützliche Begleiter.
Fazit: Ob als Bruch, Dezimalzahl oder ganze Zahl geschrieben, Null bleibt rational – und genau diese Konsistenz macht sie so nützlich.
Häufige Missverständnisse über Null: Division, Grenzwerte und „knifflige“ Fälle
Die größte Verwirrung um Null entsteht durch das Vermischen getrennter Regeln. Die klassische Falle ist die Verwechslung von „Division durch Null ist undefiniert“ mit „Null ist nicht rational“. Diese haben nichts miteinander zu tun. Bei einem Bruch p/q ist der einzige verbotene Fall q = 0. Setzt man p = 0, ist das erlaubt und ungefährlich. Maya nutzt eine schnelle Analogie: Ein Nenner von Null ist wie das Verlangen nach Plätzen auf einem Flug, der nicht existiert – keine Bordkarte hilft. Aber ein Zähler von Null bedeutet nur, dass keine Passagiere erschienen sind; der Flug existiert weiterhin.
Grenzwerte bringen den nächsten Knoten. Betrachte lim (x→0) 1/x. Von der positiven Seite nähert es sich +∞; von der negativen Seite stürzt es auf −∞. Das sagt etwas über das Verhalten nahe Null aus, nicht über den Wert von Null oder ihre Rationalität. Ähnlich tauchen in der Analysis „unbestimmte Formen“ wie 0/0 bei Grenzwertberechnungen auf, aber der Ausdruck 0/0 ist als Zahl nicht definiert. Keine dieser analytischen Ideen hebt die Zugehörigkeit von Null zur Rationalen Menge auf.
Andere knifflige Punkte zeigen sich in Kombinatorik und Algebra. Die Fakultät 0! ist definitionsgemäß 1 (im Einklang mit Rekursion und leerem Produkt), was rational ist. Exponentiation wirkt ebenfalls merkwürdig: 0^0 ist in vielen Kontexten undefiniert, weil konkurrierende Erweiterungen erwünschte Eigenschaften widersprechen würden; in der diskreten Mathematik wird sie manchmal als 1 genommen, um Formeln zu vereinfachen. Unabhängig von diesen Randregeln bleibt der Wert 0 rational.
- 🧯 Mythos: „Division durch Null beweist, dass 0 nicht rational ist.“ Realität: Nur Nenner dürfen nicht 0 sein; Zähler schon.
- 📉 Mythos: „Grenzwerte bei 0 definieren, was Null ‚ist‘.“ Realität: Grenzwerte beschreiben das Verhalten in der Nähe, nicht die Identität von Null.
- 🧩 Fakt: 0! = 1 → rational; 0^0 ist kontextabhängig, beeinflusst Nulls Rationalität nicht.
- 🔄 Fakt: Periodische Dezimalzahlen weisen Rationalität hin; Nulls Dezimalzahl ist eine triviale Wiederholung von 0.
- 🧭 Profi-Tipp: Regeln der Arithmetik, Grenzwertsätze und Mengendefinitionen getrennt im Kopf ablegen.
| Ausdruck/Idee 🧠 | Status | Auswirkung auf Nulls Rationalität 🎯 | Schülertipp ✍️ |
|---|---|---|---|
| 5/0 | Undefiniert ❌ | Keine; hat nichts damit zu tun, ob 0 rational ist. | Nenner darf nicht 0 sein. Punkt. |
| 0/5 | Gültig ✅ | Bestätigt 0 als rationale Zahl. | Jeder von null verschiedene Nenner funktioniert. |
| lim (x→0) 1/x | Kein endlicher Grenzwert | Klassifiziert 0 nicht; beschreibt Verhalten in der Nähe von 0. | Analysis von Arithmetik trennen. |
| 0! | Gleich 1 | Rational (1/1) ✅ | Leerprodukt-Konvention. |
| 0^0 | Kontextabhängig | Keine Änderung des Status von Null | Beachten Sie Ihre Kursregeln. |
Wenn mentale Modelle geschärft werden müssen, helfen gut strukturierte Arbeitsabläufe. Artikel zur Verbesserung der Evaluationsdisziplin, wie Messung dessen, was in 2025 im Unterricht zählt, oder zur Bewältigung von Kontextwechseln, etwa mit Verwaltung von Kontextfenstern, zeigen, wie sorgfältige Definitionen Kategoriefehler vermeiden. Klare Kategorien halten Null rational und verhindern eine Division durch Null – zwei Wahrheiten, die gut nebeneinander existieren.

Brücke zur Geschichte und zu Axiomen
Schüler fragen oft: Wenn die Regeln so ordentlich sind, warum hatte die Menschheit damals Schwierigkeiten, Null zu übernehmen? Das ist die perfekte Überleitung zur Geschichte von Platzhaltern, Händlern und den Axiomen, die die heutigen Definitionen festigten.
Von antiken Platzhaltern zu modernen Axiomen: Wie Null ihren Platz erhielt
Der Weg der Null von „nichts“ zu einer vollwertigen Zahl war alles andere als sofortig. Babylonische Schreiber nutzten ein Platzhaltersymbol, um Stellenwert richtig zu halten, aber das Konzept der Null als eigenständige Zahl entstand in Indien, mit Mathematikern wie Brahmagupta, die um das 7. Jahrhundert die Arithmetik mit Null formulierten. Handel und Wissenschaft trugen diese Ideen durch die islamische Welt nach Europa, wo der Widerstand allmählich nachließ, als sich die Stellenwertnotation im Handel und in der Astronomie als unverzichtbar erwies. Der Aufstieg von Algebra und später Analysis verankerte Nulls zentrale Rolle.
Moderne axiomatische Ansätze machen die Klassifizierung wasserdicht. Ausgehend von Strukturen wie den Peano-Axiomen für natürliche Zahlen konstruieren Mathematiker ganze Zahlen aus Äquivalenzklassen von Zahlenpaaren und rationale Zahlen aus Äquivalenzklassen ganzer Zahlenpaare (p, q) mit q ≠ 0. In dieser Konstruktion repräsentiert die Klasse [(0, 1)] die rationale Zahl 0 – klar und eindeutig. Deshalb sagen Lehrbücher ohne Zögern, dass Null rational ist. Der einzige Knackpunkt ist, ob „natürliche Zahlen“ Null einschließen; beides ist konsistent, aber Lehrkräfte sollten ihre Konvention benennen.
Maya verwendet eine kurze Zeitleiste, um Lernenden den Wandel zu verankern. So fühlt sich die heutige Definition an wie das Ende eines langen Ingenieursprojekts: Die Teile fügen sich, weil sie so entworfen wurden.
- 📜 Platzhalter im antiken Babylon bereiteten die Stellenwertrechnung vor.
- 🧮 Indische Mathematiker formalisierten die Arithmetik mit Null und negativen Zahlen.
- 🌍 Wissensaustausch durch Handel verfestigte 0 in der globalen Mathematik.
- 🏛️ Axiomatische Systeme leiteten rationale Zahlen von ganzen mit q ≠ 0 ab.
- 🔧 Informatik und Datenwissenschaft standardisierten die Rolle der Null in Indizes und Logik.
| Epoche ⏳ | Meilenstein | Auswirkung auf Rationalität von 0 🎯 | Gedächtnishilfe 📌 |
|---|---|---|---|
| Antike | Platzhalter entsteht | Bereitet stellwertorientiertes Denken vor, noch keine Zahl | „Leerplatz“ in der Zahlenreihe |
| Klassisches Indien | 0 als Zahl mit Operationen | Arithmetikregeln stabilisieren sich | 0 × a = 0, a + 0 = a |
| Mittelalterliche Weitergabe | Handel und Wissenschaft verbreiten Stellenwert | Notation wird standardisiert | Händler brauchen Nullen |
| Moderne Axiome | Bau von ℚ aus ganzen Zahlenpaaren (p, q) | [(0, 1)] ist rationale 0 ✅ | q ≠ 0 ist einzige Beschränkung |
Heutige Pädagog:innen kombinieren oft historischen Kontext mit digitalen Werkzeugen für besseren Lernerhalt. Schulblogs, die sensible Technikgeschichten aufbereiten – etwa rechtliche Debatten um KI – zeigen, warum präzise Definitionen wichtig sind. Ähnlich unterstützen Vergleiche von Assistenten, wie Copilot gegen ChatGPT, die Idee, dass konsistente Regeln zu vertrauenswürdigen Ergebnissen führen. Sogar Diskussionen über Datenverarbeitung und Dateianalyse untermauern die Lehre: Saubere Eingaben und klare Beschränkungen – wie q ≠ 0 – halten Systeme stabil.
Fazit für Lernende: Null entstand nicht einfach so; sie wurde in das Zahlensystem hineingekonstruert, und ihr rationaler Status ist von Anfang an gesichert.
Praxisnahes Denken: Zahlen schnell klassifizieren (mit Null als Anker)
Mit dem Gesamtüberblick führt Maya einen „90-Sekunden-Sortierer“ für Übungsaufgaben ein. Die Idee ist, jede Eingabe schnell zu klassifizieren, indem man die Bruchform, das Dezimalverhalten und die Mengenmitgliedschaft prüft – mit Null als Ankerfall. Ziel ist Geschwindigkeit ohne Schlamperei. Lernende können sogar ein Mini-Spickzettel für Prüfungsränder anfertigen.
Beginnen Sie mit dem Bruchtest. Ist die Zahl p/q mit ganzzahligem p, q und q ≠ 0? Wenn ja, ist sie rational. Hat die Dezimalzahl eine endliche oder periodische Darstellung (wie 0,125 oder 0,333…), ist sie rational. Ist sie weder terminierend noch periodisch (wie π oder √2 als Dezimalzahlen), ist sie irrational. Bei ganzen Zahlen gilt: n = n/1, also ist jede ganze Zahl rational; somit ist 0 rational, da 0 = 0/1. Diese Prüfungen gelten einheitlich über alle Aufgaben.
- 🧩 Schritt 1: Versuche p/q mit ganzzahligen Teilen; lehne q = 0 sofort ab.
- 🔎 Schritt 2: Prüfe Dezimalzahlen: terminierend oder periodisch → rational.
- 🧱 Schritt 3: Ganze Zahlen qualifizieren automatisch (n = n/1), auch 0.
- 🛑 Schritt 4: Wenn keines zutrifft und Dezimalzahlen nicht wiederholen → irrational.
- 🗂️ Schritt 5: Notiere Mengenmitgliedschaft (voll, ganz, reell) für volle Punkte.
| Wert 🔢 | Bruchform | Rational? ✅/❌ | Set-Tags 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | Ganzzahl, Vollzahl, Reell |
| −3/4 | −3/4 | ✅ | Rational, Reell |
| 0,125 | 1/8 | ✅ | Rational, Reell |
| 0,333… | 1/3 | ✅ | Rational, Reell |
| √2 | — | ❌ | Irrational, Reell |
| π | — | ❌ | Irrational, Reell |
Wollen Sie audiovisuelle Unterstützung? Ein kurzes Erklärvideo kann die Grenze zwischen rational und irrational festigen und dabei Null ins Rampenlicht stellen. Lehrkräfte, die Wiedergabelisten erstellen, können strukturierte Abfragen nutzen, um prägnante Clips auszuwählen.
Technisch versierte Lernende probieren oft Notizsysteme und Pipelines aus; wenn das Ihr Stil ist, können modulare Arbeitsabläufe wie virtualisierte Medienserver Studienressourcen hosten, und Aufgaben-Automatisierung via API-Tools können Übungskarten zu kniffligen Grenzfällen wie 0, 0/0 (undefiniert) und 1/0 (undefiniert) automatisch erzeugen. Eine saubere Pipeline unterstützt eine klare Definition.
Abschließender Gedanke zu diesem Abschnitt: Konsistenz gewinnt. Null verhält sich in allen Darstellungen gleich und ist somit der perfekte Anker für den Sortierer.
Besondere Anwendungen: Stellenwert, Datensysteme und Unterrichtsgeschichten, bei denen Null wichtig ist
Die Rationalität von Null ist nicht nur ein Beweis; sie stützt, wie Informationssysteme und Lehrpläne funktionieren. Im Dezimalsystem signalisiert die Ziffer 0 „keine dieser Stelle“, was die korrekte Größenordnung bewahrt: 101 unterscheidet sich von 11, weil die mittlere 0 den Zehnerplatz leer lässt. In Tabellenkalkulationen und Programmen steht eine Null oft für „keine Elemente“, „kein Fehler“ oder Basiswert – das macht Berechnungen determiniert. Uneinheitlicher Umgang mit 0 würde Chaos in Dashboards, Zeitberechnungen und Algorithmen bringen.
Betrachten Sie Datenklassifikationsaufgaben: Wenn eine Spalte nur rationale Zahlen speichern soll, muss Null zugelassen werden, sonst würden legitime Basis-Messwerte abgelehnt. Maya entwirft eine kleine „Datenhygiene“-Demo: Ein Parser bekommt eine Mischung aus ganzen Zahlen, einfachen Brüchen, periodischen Dezimalzahlen und bekannten irrationalen Zahlen; der Validator akzeptiert alles, was in p/q mit q ≠ 0 konvertierbar ist. Die Demo protokolliert 0 als gültig über ganzzahlige und Bruchpfade. Danach schreiben Schüler Unit-Tests, um die Abgeschlossenheit bei Addition und Multiplikation mit Null zu bestätigen.
- 🧮 Stellenwert: 0 hält Ziffern ausgerichtet und verhindert Größenordnungsfehler.
- 🧰 Datensicherheit: Null muss in rational-only Feldern validieren.
- 🧷 Fehlermanagement: 1/0-Fehler werden beim Parsen, nicht zur Laufzeit, erkannt.
- 🧪 Testen: Null in allen Abgeschlossenkeits-Tests der Rationalen einbeziehen.
- 📚 Storyline: Maya bezeichnet 0 als „den Anker“ in Bewertungsrastern und Projektdokumentationen.
| Szenario 🗂️ | Nulls Rolle | Warum Rationalität hilft 🎓 | Unterrichtshinweis 🛎️ |
|---|---|---|---|
| Stellenwert | Füllt leere Positionen | Konsistente Größenordnungserklärung | „0 hält den Platz warm“ 😊 |
| Validierung | Akzeptiert als 0/1 | Saubere Eingabebeschränkungen | Teste 0, 1/0, 0/0 getrennt |
| Berechnung | Additives Identitätselement | Vereinfacht Beweise und Code | Setze 0 in Unit-Tests ein |
| Unterricht | Ankerfall | Verhindert Mythen und Verwirrung | Beginne Beispiele mit 0 |
Kurze Neugierdepause: Kommunikation rund um Mathematik profitiert von präziser Sprache und Kontext. Auch außerhalb der Mathematik zählt Klarheit – sei es beim Deuten von Emoji-Bedeutungen für Ton in Foren, beim Bewerten von Schulsicherheitstechnik oder beim Erkennen von Nachrichten-Narrativen. Die Lehre gilt überall: Definitionen, Beschränkungen und Beispiele verhindern Missverständnisse. Ebenso erinnert ein scheinbar harmloser Abstecher wie Symbolinterpretationen Lernende daran, wie schnell Bedeutung ohne gemeinsame Regeln wandern kann – genau deshalb hält die rationale Definition Null fest verankert.
Schlussgedanke in diesem Abschnitt: Nulls Rationalität ist mehr als ein Label; sie garantiert, dass Systeme – von Arithmetik bis Analytik – vorhersehbar bleiben.
Extra Übung mit Mayas Mini-Set
Mayas Schüler klassifizieren diese Zahlen in unter einer Minute: 0, −7, 2/9, 0/3, 3/0, 0,1010010001…, und √9. Die Ergebnisse: 0 (rational), −7 (rational), 2/9 (rational), 0/3 (rational), 3/0 (undefiniert), 0,1010010001… (nicht periodisch, nicht terminierend → vermutlich irrational), √9 (gleich 3 → rational). Die Fähigkeit zum Mustererkennen überträgt sich auf weitere Einheiten und Tests.
{“@context”:”https://schema.org”,”@type”:”FAQPage”,”mainEntity”:[{“@type”:”Question”,”name”:”Is zero considered a rational number?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Yes. By definition, a rational number is any value expressible as p/q with integers p and q and q u2260 0. Zero fits because 0 = 0/1, 0/5, or 0/n for any nonzero integer n.”}},{“@type”:”Question”,”name”:”Does division by zero make zero non-rational?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”No. Division by zero is a rule about denominators, not about the number zero. 5/0 and 0/0 are undefined expressions, but 0 itself remains a valid rational number.”}},{“@type”:”Question”,”name”:”Is zero an integer, whole, or natural number?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Zero is an integer and a whole number. Whether it is a natural number depends on convention: many courses start naturals at 1, while some contexts include 0.”}},{“@type”:”Question”,”name”:”Can zero be written as a decimal and still be rational?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Yes. Zerou2019s decimal form is 0.0 (or 0.000u2026), which is terminating. Terminating and repeating decimals are rational by definition.”}},{“@type”:”Question”,”name”:”How does zerou2019s role help in algebra?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Zero is the additive identity: a + 0 = a. It keeps equations balanced and simplifies proofs. Multiplying any rational number by 0 gives 0, which is rational.”}}]}Ist Null eine rationale Zahl?
Ja. Per Definition ist eine rationale Zahl jeder Wert, der als p/q mit ganzzahligen p und q und q ≠ 0 dargestellt werden kann. Null passt, weil 0 = 0/1, 0/5 oder 0/n für jede von null verschiedene ganze Zahl n gilt.
Macht Division durch Null Null nicht rational?
Nein. Division durch Null ist eine Regel für Nenner, nicht für die Zahl Null. 5/0 und 0/0 sind undefinierte Ausdrücke, aber 0 selbst bleibt eine gültige rationale Zahl.
Ist Null eine ganze Zahl, volle Zahl oder natürliche Zahl?
Null ist eine ganze Zahl und eine volle Zahl. Ob sie eine natürliche Zahl ist, hängt von der Konvention ab: Viele Kurse beginnen die natürlichen Zahlen bei 1, während manche Kontexte 0 einschließen.
Kann Null als Dezimalzahl geschrieben werden und trotzdem rational sein?
Ja. Die Dezimaldarstellung von Null ist 0,0 (oder 0,000…), was terminierend ist. Terminierende und periodische Dezimalzahlen sind per Definition rational.
Wie hilft Nulls Rolle in der Algebra?
Null ist das additive Identitätselement: a + 0 = a. Sie hält Gleichungen im Gleichgewicht und vereinfacht Beweise. Das Multiplizieren jeder rationalen Zahl mit 0 ergibt 0, was rational ist.

-

 Tech2 days ago
Tech2 days agoIhre Karte unterstützt diesen Kaufart nicht: was das bedeutet und wie Sie das Problem lösen können
-

 KI-Modelle1 day ago
KI-Modelle1 day agoOpenAI vs Tsinghua: Die Wahl zwischen ChatGPT und ChatGLM für Ihre KI-Bedürfnisse im Jahr 2025
-

 Internet23 hours ago
Internet23 hours agoDie Zukunft erkunden: Was Sie über internetfähiges ChatGPT im Jahr 2025 wissen müssen
-

 KI-Modelle1 day ago
KI-Modelle1 day agoDie Wahl Ihres KI-Forschungspartners im Jahr 2025: OpenAI vs. Phind
-

 Tech11 hours ago
Tech11 hours agoDas Verständnis von hart degeneriert: was es bedeutet und warum es 2025 wichtig ist
-

 Gaming18 hours ago
Gaming18 hours agoKostenloser Kampf-nyt: Strategien, um den ultimativen Kampf zu meistern