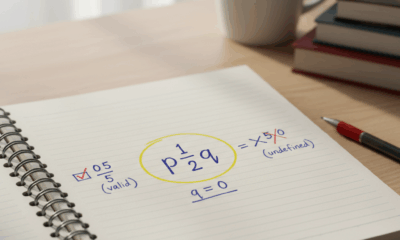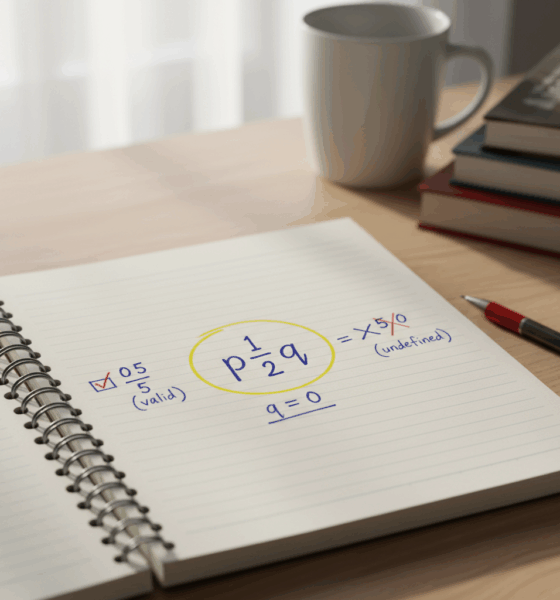
Tecnologia
0 é considerado um número racional? explicado de forma simples
O Zero é Considerado um Número Racional? Uma Explicação Simples que Fica
Pergunte a qualquer estudante que está lutando com frações: o zero é um número racional? A resposta clara em matemática é sim. Um número racional é qualquer valor que pode ser escrito como uma fração p/q onde p e q são números inteiros, e o denominador q não é zero. Como 0 pode ser expresso como 0/1, 0/7 ou, mais geralmente, 0/n para qualquer inteiro n diferente de zero, ele se encaixa perfeitamente. Mas a história fica mais rica quando a lente se amplia para a teoria dos números, limites e como os aprendizes internalizam conceitos matemáticos. Para manter as coisas relacionáveis, conheça Maya, uma programadora de escola secundária que dá aulas para crianças mais novas; ela adora uma explicação simples respaldada por exemplos nítidos e identificação de padrões.
Maya começa com uma lista rápida. Se um número tem uma forma fracionária válida com numerador inteiro e denominador não zero, ele é racional. Zero passa porque seu numerador pode ser 0 enquanto seu denominador pode ser qualquer inteiro diferente de zero. Divisão por zero é proibida, mas essa regra se refere ao denominador, não ao número zero em si. Na aula, essa distinção evita a confusão clássica: 0/5 é válido (e equivale a 0), enquanto 5/0 é indefinido. Essa única linha salva horas de confusão.
Para os aprendizes que gostam de contexto, zero também está incluído em outros conjuntos. É um inteiro (…−2, −1, 0, 1, 2…), um número inteiro não negativo (0, 1, 2, 3, …) e um número real (parte do continuum completo incluindo valores racionais e irracionais). No entanto, muitos livros definem números naturais como começando em 1, o que exclui 0; alguns contextos de ciência da computação incluem 0 como natural. Saber qual convenção um curso usa evita debates desnecessários.
Nas salas de aula de 2025, os professores usam cada vez mais IA e explicadores para tornar essas distinções memoráveis. Ferramentas que ajudam a organizar exemplos — como quadros de projeto e planejadores de conteúdo — espelham a clareza das definições de frações. Para um vislumbre de como ferramentas de pensamento estruturado estão remodelando fluxos de aprendizado, recursos sobre automação com APIs ou um panorama sobre tendências tecnológicas centradas na educação ilustram como a clareza escala. Até explorações curiosas — como o que um bilhão de segundos parece — podem contextualizar números grandes e pequenos que aparecem em aulas sobre frações e valor posicional.
- ✅ Zero é racional porque equivale a 0/n com n ≠ 0.
- 🚫 Divisão por zero (como 5/0) é indefinida, não relacionada à racionalidade do zero.
- 🧩 Zero pertence a múltiplos conjuntos: inteiro, inteiro não negativo e números reais.
- 🧠 Convenções variam para números naturais; verifique a definição do seu curso.
- 🎯 Use o teste da fração: numerador inteiro e denominador não zero.
| Número 🔢 | Racional? ✅/❌ | Razão 💡 |
|---|---|---|
| 0 | ✅ | Pode ser escrito como 0/1, 0/5, … com partes inteiras e denominador não zero. |
| 5 | ✅ | Equivale a 5/1 (forma fracionária inteira). |
| 1/3 | ✅ | Numerador e denominador inteiros; decimal é periódico. |
| π | ❌ | Não pode ser expresso como razão de inteiros; decimal é não periódico. |
| √2 | ❌ | Provado irracional; nenhuma fração inteira equivale a √2. |
Insight chave para levar adiante: a definição de fração sozinha resolve o status do zero — sem drama, apenas estrutura.

Da Forma Fracionária aos Usos Reais do Zero
Antes de entrar nas propriedades, Maya faz uma pergunta prática: onde o zero aparece fora das planilhas? Em orçamentos, uma linha zero significa nenhum gasto; em códigos, 0 indica falso ou vazio; em painéis de dados, 0 marca a linha de base. A mesma clareza necessária para tratar 0 como racional ajuda equipes a rotular, comparar e calcular sem ambiguidades. Para desenvolvedores que experimentam utilitários de tempo, entender o zero como um offset inicial se alinha com ferramentas confiáveis como recuperação precisa de tempo em Swift para aritmética de intervalos.
Por que 0 Encaixa na Definição de Número Racional: Frações, Decimais e Álgebra
Além da definição formal, a versatilidade do zero como número racional emerge em múltiplas representações. Em qualquer fração p/q, se p = 0 e q ≠ 0, o valor é 0. Por isso 0/1 = 0/9 = 0/−13 = 0. Trocar sinais ou mudar o denominador não altera o valor porque multiplicar ou dividir zero por qualquer inteiro diferente de zero ainda resulta em zero. Isso faz do 0 o valor mais estável da fração sob transformações equivalentes.
Decimais contam a mesma história. Um número racional tem expansão decimal finita ou periódica. O decimal do zero é 0,0, 0,000… ou qualquer sequência equivalente com zeros finitos ou infinitos depois — todas opções são, na prática, finitas. Se um estudante vê 0,000, o essencial é que não há dígitos diferentes de zero após a vírgula; portanto, é racional e equivale a 0.
Álgebra aprofunda a intuição. Zero é a identidade aditiva: para qualquer número a, a + 0 = a. Essa identidade combina bem com regras da aritmética racional. Por exemplo, adicionar 0 a um racional p/q mantém p/q racional. Multiplicar qualquer racional por 0 dá 0, que novamente é racional. As propriedades de fechamento dos números racionais e o papel especial do 0 se reforçam mutuamente: nada se quebra quando zero entra na festa.
Maya demonstra com uma rotina de sala de aula que os aprendizes podem copiar em notas ou flashcards. A rotina evita atalhos e destaca as regras que realmente importam.
- 🧪 Teste da fração: escreva o número como p/q com inteiros p, q e q ≠ 0 → racional.
- 🔁 Teste decimal: finito ou periódico → racional (decimal do zero é todo zero).
- ➕ Cheque da identidade: adicionar 0 não muda nada; multiplicar por 0 retorna 0.
- 🧭 Sanidade dos sinais: 0/−7 = 0/7 = 0; o sinal no denominador não importa.
- ⚠️ Alerta: denominador 0 torna expressão indefinida, não “irracional.”
| Representação 🧮 | Exemplo | Racional? 🔍 | Razão 🧠 |
|---|---|---|---|
| Fração | 0/19 | ✅ | Numerador inteiro e denominador não zero → valor é 0. |
| Decimal | 0,000… | ✅ | Decimal finito (ou efetivamente finito). |
| Forma inteira | 0 | ✅ | Todo inteiro é racional (n = n/1). |
| Número misto | 0 0/5 | ✅ | Equivale a 0; a parte fracionária desaparece. |
| Notação científica | 0,0 × 10³ | ✅ | Ainda 0; notação não afeta racionalidade. |
Para aprendizes que gostam de cruzar com tecnologia, treinadores de rascunho com IA podem ajudar explicadores a permanecer consistentes; veja como um treinador de escrita para clareza ou bibliotecas curadas para saídas estruturadas espelham a confiabilidade das regras de fração. E se o progresso precisa ser monitorado por semanas, utilitários como contadores baseados em calendário são companheiros úteis.
Conclusão: seja escrito como fração, decimal ou inteiro, o zero permanece racional — e essa consistência é exatamente o que o torna tão útil.
Conceitos Equivocados Comuns Sobre o Zero: Divisão, Limites e Casos “Difíceis”
A maior confusão sobre zero vem de misturar regras distintas. A armadilha clássica é confundir “divisão por zero é indefinida” com “zero não é racional.” Não têm nenhuma relação. Em uma fração p/q, o único movimento proibido é q = 0. Definir p = 0 é permitido e inofensivo. Maya usa uma analogia rápida: denominador zero é como pedir assentos em um voo que não existe — nenhum cartão de embarque resolve. Mas ter numerador zero só significa que não há passageiros; o voo ainda existe.
Limites criam o próximo nó. Considere lim (x→0) 1/x. Aproximando-se pelo lado positivo corre para +∞; pelo lado negativo, cai para −∞. Isso nos diz algo sobre o comportamento próximo de zero, não sobre o valor de zero ou sua racionalidade. Similarmente, “formas indeterminadas” como 0/0 aparecem no cálculo ao avaliar limites, mas a expressão 0/0 é indefinida como número. Nenhuma dessas ideias analíticas revoga a pertença do zero ao conjunto dos racionais.
Outros pontos complicados surgem em combinatória e álgebra. O fatorial 0! é igual a 1 por definição (consistente com recursão e lógica do produto vazio), que é racional. Exponenciação também pode parecer estranha: 0^0 é indefinido em muitos contextos porque extensões concorrentes contradizem propriedades desejáveis; em matemática discreta, às vezes é tomado como 1 para simplificar fórmulas. Independentemente dessas regras de exceção, o valor 0 permanece racional.
- 🧯 Mito: “Divisão por zero prova que 0 não é racional.” Realidade: somente denominadores não podem ser 0; numeradores podem.
- 📉 Mito: “Limites em 0 definem o que zero ‘é’.” Realidade: limites descrevem comportamento próximo, não identidade do zero.
- 🧩 Fato: 0! = 1 → racional; 0^0 é sensível ao contexto, mas não afeta racionalidade do zero.
- 🔄 Fato: Decimais periódicos indicam racionalidade; decimal de zero é repetição trivial de 0s.
- 🧭 Dica profissional: mantenha regras aritméticas, leis de limites e definições de conjuntos em gavetas mentais separadas.
| Expressão/Ideia 🧠 | Status | Impacto na Racionalidade do Zero 🎯 | Dica para Estudante ✍️ |
|---|---|---|---|
| 5/0 | Indefinido ❌ | Nenhum; não relacionado a se 0 é racional. | Denominador não pode ser 0. Ponto final. |
| 0/5 | Válido ✅ | Confirma 0 como número racional. | Qualquer denominador diferente de zero funciona. |
| lim (x→0) 1/x | Sem limite finito | Não classifica 0; fala sobre comportamento próximo a 0. | Separe cálculo de aritmética. |
| 0! | Igual a 1 | Racional (1/1) ✅ | Convenção do produto vazio. |
| 0^0 | Dependente do contexto | Sem mudança no status do zero | Siga as regras do seu curso. |
Quando modelos mentais precisam ser afinados, fluxos de trabalho bem estruturados ajudam. Artigos sobre melhorar disciplina de avaliação, como medindo o que importa em salas de aula de 2025, ou lidando com mudanças de contexto, como em gerenciamento de janelas de contexto, mostram como definições cuidadosas previnem erros de categoria. Categorias claras são exatamente o que mantêm o zero racional e a divisão por zero proibida — duas verdades que coexistem felizmente.

Ponte para História e Axiomas
Estudantes perguntam frequentemente: se as regras são tão organizadas, por que a humanidade demorou para adotar o zero? Esse é o gancho perfeito para a história dos marcadores de posição, mercadores e axiomas que consolidaram as definições atuais.
De Marcadores de Posição Antigos a Axiomas Modernos: Como o Zero Ganhou Seu Lugar
O caminho do zero de “nada” a um número completo não foi imediato. Escribas babilônicos usavam um símbolo marcador para manter o valor posicional correto, mas o conceito de zero como número independente surgiu na Índia, com matemáticos como Brahmagupta articulando a aritmética com zero por volta do século VII. O comércio e a erudição levaram essas ideias para o mundo islâmico e para a Europa, onde a resistência foi gradualmente diminuindo conforme a notação posicional provava ser indispensável no comércio e na astronomia. O surgimento da álgebra, e depois do cálculo, consolidou a centralidade do zero.
Abordagens axiomáticas modernas tornam a classificação à prova de falhas. Começando com estruturas como os axiomas de Peano para números naturais, os matemáticos constroem inteiros a partir de classes de equivalência de pares de naturais, e racionais a partir de classes de equivalência de pares inteiros (p, q) com q ≠ 0. Nessa construção, a classe [(0, 1)] representa o número racional 0 — limpo e sem ambiguidades. Por isso os livros afirmam sem hesitar que zero é racional. A única variação está em se “números naturais” incluem zero; ambas escolhas são consistentes, mas os professores devem declarar sua convenção.
Maya usa uma linha do tempo curta para ajudar aprendizes a ancorar a evolução. Isso faz a definição atual parecer o fim de um longo projeto de engenharia: as peças se encaixam porque foram desenhadas assim.
- 📜 Marcadores na antiga Babilônia prepararam o caminho para a notação posicional.
- 🧮 Matemáticos indianos formalizaram a aritmética com zero e números negativos.
- 🌍 Transferência de conhecimento via comércio solidificou o zero na matemática global.
- 🏛️ Configurações axiomáticas derivaram números racionais a partir de inteiros com q ≠ 0.
- 🔧 Computação e ciência de dados padronizaram o papel do zero em indexação e lógica.
| Era ⏳ | Marco | Impacto na Racionalidade do 0 🎯 | Gancho de Memória 📌 |
|---|---|---|---|
| Antiguidade | Marcador emerge | Prepara pensamento posicional mas ainda não é número | “Assento vazio” na linha numérica |
| Índia Clássica | 0 como número com operações | Regras aritméticas estabilizam | 0 × a = 0, a + 0 = a |
| Transmissão medieval | Comércio e erudição espalham valor posicional | Notação se padroniza | Mercadores precisam do zero |
| Axiomas modernos | Constroem ℚ a partir de inteiros via pares (p, q) | [(0, 1)] é 0 racional ✅ | q ≠ 0 é a única restrição |
Educadores hoje mesclam contexto histórico com ferramentas digitais para melhorar a retenção. Blogs de sala de aula que explicam histórias sensíveis de tecnologia — como debates jurídicos envolvendo IA — mostram como definições precisas importam. Da mesma forma, textos comparando assistentes, como Copilot vs. ChatGPT, reforçam a ideia de que regras consistentes levam a resultados confiáveis. Até discussões sobre manuseio de dados e análise de arquivos reforçam a lição: entradas limpas e restrições claras — como q ≠ 0 — mantêm sistemas estáveis.
Conclusão para aprendizes: o zero não apareceu do nada; foi construído no sistema numérico, e seu status racional é garantido pela construção.
Raciocínio Prático: Classificando Números Rapidamente (Com o Zero como Base)
Com o panorama geral definido, Maya realiza um “separador de 90 segundos” para conjuntos de problemas. A ideia é classificar qualquer entrada rapidamente verificando forma fracionária, comportamento decimal e inclusão em conjuntos — usando zero como caso base. O objetivo é velocidade sem descuido. Os aprendizes podem até criar um mini resumo para as margens das provas.
Comece com o teste da fração. Pode ser p/q com inteiros p, q e q ≠ 0? Se sim, é racional. Se a forma decimal termina ou repete (como 0,125 ou 0,333…), é racional. Se não termina nem repete (como π ou √2 em decimal), é irracional. Para inteiros, lembre que n = n/1 faz todo inteiro racional; assim, 0 é racional porque 0 = 0/1. Esses testes valem para todos os exercícios.
- 🧩 Passo 1: Tente p/q com partes inteiras; rejeite q = 0 imediatamente.
- 🔎 Passo 2: Inspecione decimais: finito ou periódico → racional.
- 🧱 Passo 3: Inteiros se qualificam automaticamente (n = n/1), incluindo 0.
- 🛑 Passo 4: Se não termina nem repete → irracional.
- 🗂️ Passo 5: Anote pertencimento a conjuntos (inteiro não negativo, inteiro, real) para crédito total.
| Valor 🔢 | Forma Fracionária | Racional? ✅/❌ | Etiquetas de Conjunto 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | Inteiro, Inteiro Não Negativo, Real |
| −3/4 | −3/4 | ✅ | Racional, Real |
| 0,125 | 1/8 | ✅ | Racional, Real |
| 0,333… | 1/3 | ✅ | Racional, Real |
| √2 | — | ❌ | Irracional, Real |
| π | — | ❌ | Irracional, Real |
Quer reforço audiovisual? Um vídeo explicativo rápido pode fixar a fronteira entre racional e irracional mantendo o zero como protagonista. Para professores montando playlists, consultas estruturadas podem ajudar a encontrar clipes concisos.
Aprendizes ligados em tecnologia frequentemente prototipam sistemas de notas e pipelines; se esse é seu estilo, fluxos modulares como servidores de mídia virtualizados podem hospedar recursos de estudo, e automação via ferramentas API podem gerar automaticamente conjuntos de prática focados em casos de fronteira complicados como 0, 0/0 (indefinido) e 1/0 (indefinido). Um pipeline limpo reforça uma definição limpa.
Pensamento final para esta seção: consistência vence. Zero se comporta do mesmo modo em todas as representações, tornando-se a âncora perfeita para o separador.
Aplicações de Borda: Valor Posicional, Sistemas de Dados e Narrativas em Sala Onde o Zero Importa
A racionalidade do zero não é apenas uma prova; ela sustenta como sistemas de informação e currículos funcionam. No sistema posicional decimal, o dígito 0 sinaliza “nenhuma unidade naquela casa,” o que mantém a magnitude correta: 101 é diferente de 11 porque o zero do meio preserva a casa das dezenas vazia. Em planilhas e códigos, zero muitas vezes indica “nenhum item,” “sem erro” ou linha de base — tornando cálculos determinísticos. Um tratamento desorganizado do 0 injetaria caos em dashboards, matemática de tempo e algoritmos.
Considere tarefas de classificação de dados: se uma coluna deve armazenar apenas números racionais, zero precisa ser admitido, ou medições legítimas na linha de base seriam rejeitadas. Maya cria uma pequena demonstração de “higiene de dados”: alimentar um analisador com uma mistura de inteiros, frações simples, decimais periódicos e irracionais conhecidos; o validador aceita qualquer coisa conversível em p/q com q ≠ 0. A demonstração registra 0 como válido em caminhos inteiro e fracionário. A partir daí, os estudantes escrevem testes unitários para confirmar fechamento sob adição e multiplicação com zero.
- 🧮 Valor posicional: 0 mantém dígitos alinhados, prevenindo erros de magnitude.
- 🧰 Integridade de dados: zero deve ser validado em campos só de números racionais.
- 🧷 Tratamento de erros: erros 1/0 são capturados na análise, não em tempo de execução.
- 🧪 Testes: inclua 0 em todos os testes de propriedades de fechamento para racionais.
- 📚 Narrativa: Maya rotula 0 como “a âncora” em rúbricas e documentos de projeto.
| Cenário 🗂️ | Papel do Zero | Por que a Racionalidade Ajuda 🎓 | Dica em Sala 🛎️ |
|---|---|---|---|
| Valor posicional | Segura posições vazias | Interpretação consistente de magnitude | “0 mantém o lugar aquecido” 😊 |
| Validação | Aceito como 0/1 | Restrições limpas na entrada | Teste 0, 1/0, 0/0 separadamente |
| Cálculo | Identidade aditiva | Simplifica provas e códigos | Use 0 em testes unitários |
| Ensino | Caso âncora | Reduz propagação de equívocos | Comece exemplos com 0 |
Pausa para curiosidade: comunicação sobre matemática se beneficia de linguagem precisa e contexto. Mesmo fora da matemática, clareza importa — seja para interpretar significados de emojis para tom em fóruns estudantis, avaliar tecnologias de segurança escolar, ou detectar narrativas de notícias. A lição se transfere: definições, restrições e exemplos previnem confusões. Do mesmo modo, uma curiosidade inofensiva como interpretação de símbolos lembra como o significado pode mudar rapidamente sem regras compartilhadas — exatamente por isso a definição racional mantém o zero firme.
Insight final deste segmento: a racionalidade do zero é mais do que um rótulo; é uma garantia de que sistemas — da aritmética à análise — permanecem previsíveis.
Prática Extra com o Mini-Conjunto da Maya
Os estudantes da Maya classificam estes em menos de um minuto: 0, −7, 2/9, 0/3, 3/0, 0,1010010001…, e √9. Os resultados: 0 (racional), −7 (racional), 2/9 (racional), 0/3 (racional), 3/0 (indefinido), 0,1010010001… (não periódico, não finito → provavelmente irracional), √9 (igual a 3 → racional). A habilidade de identificar padrões se transfere por unidades e provas.
{“@context”:”https://schema.org”,”@type”:”FAQPage”,”mainEntity”:[{“@type”:”Question”,”name”:”Is zero considered a rational number?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Yes. By definition, a rational number is any value expressible as p/q with integers p and q and q u2260 0. Zero fits because 0 = 0/1, 0/5, or 0/n for any nonzero integer n.”}},{“@type”:”Question”,”name”:”Does division by zero make zero non-rational?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”No. Division by zero is a rule about denominators, not about the number zero. 5/0 and 0/0 are undefined expressions, but 0 itself remains a valid rational number.”}},{“@type”:”Question”,”name”:”Is zero an integer, whole, or natural number?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Zero is an integer and a whole number. Whether it is a natural number depends on convention: many courses start naturals at 1, while some contexts include 0.”}},{“@type”:”Question”,”name”:”Can zero be written as a decimal and still be rational?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Yes. Zerou2019s decimal form is 0.0 (or 0.000u2026), which is terminating. Terminating and repeating decimals are rational by definition.”}},{“@type”:”Question”,”name”:”How does zerou2019s role help in algebra?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Zero is the additive identity: a + 0 = a. It keeps equations balanced and simplifies proofs. Multiplying any rational number by 0 gives 0, which is rational.”}}]}O zero é considerado um número racional?
Sim. Por definição, um número racional é qualquer valor que pode ser expresso como p/q com inteiros p e q e q ≠ 0. O zero se encaixa porque 0 = 0/1, 0/5, ou 0/n para qualquer inteiro n diferente de zero.
A divisão por zero torna o zero não racional?
Não. A divisão por zero é uma regra sobre denominadores, não sobre o número zero. 5/0 e 0/0 são expressões indefinidas, mas o 0 em si continua sendo um número racional válido.
O zero é um número inteiro, inteiro não negativo ou natural?
O zero é um número inteiro e inteiro não negativo. Se é um número natural depende da convenção: muitos cursos consideram os naturais iniciando em 1, enquanto alguns contextos incluem o 0.
O zero pode ser escrito como decimal e ainda ser racional?
Sim. A forma decimal do zero é 0,0 (ou 0,000…), que é finita. Decimais finitos e periódicos são racionais por definição.
Como o papel do zero ajuda na álgebra?
Zero é a identidade aditiva: a + 0 = a. Mantém equações balanceadas e simplifica provas. Multiplicar qualquer número racional por 0 resulta em 0, que é racional.

-

 Tecnologia1 day ago
Tecnologia1 day agoSeu cartão não suporta este tipo de compra: o que significa e como resolver
-

 Modelos de IA1 day ago
Modelos de IA1 day agoOpenAI vs Tsinghua: Escolhendo Entre ChatGPT e ChatGLM para Suas Necessidades de IA em 2025
-

 Internet23 hours ago
Internet23 hours agoExplorando o Futuro: O Que Você Precisa Saber Sobre o ChatGPT com Internet em 2025
-

 Modelos de IA1 day ago
Modelos de IA1 day agoEscolhendo Seu Companheiro de Pesquisa em IA em 2025: OpenAI vs. Phind
-

 Tecnologia10 hours ago
Tecnologia10 hours agoCompreendendo hard degenerate: o que significa e por que importa em 2025
-

 Gaming18 hours ago
Gaming18 hours agoGrátis para todos lutar nyt: estratégias para dominar a batalha definitiva