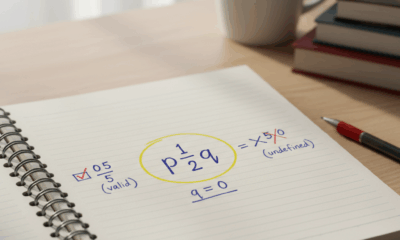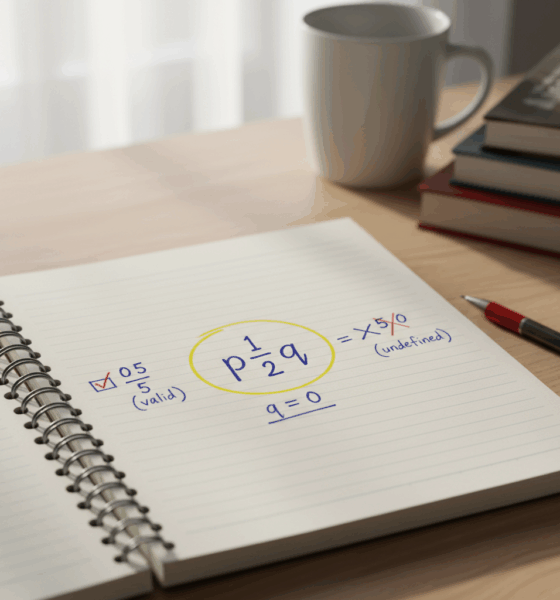
Tecnologia
¿Se considera el cero un número racional? Explicado de manera sencilla
¿Se Considera el Cero un Número Racional? Una Explicación Sencilla que Permanece
Pregúntale a cualquier estudiante que esté luchando con fracciones: ¿es cero un número racional? La respuesta clara en matemáticas es sí. Un número racional es cualquier valor que se pueda escribir como una fracción p/q donde p y q son enteros, y el denominador q no es cero. Como 0 puede expresarse como 0/1, 0/7, o más generalmente 0/n para cualquier entero n distinto de cero, encaja perfectamente. Pero la historia se vuelve más rica cuando se amplía la perspectiva a la teoría de números, los límites y cómo los estudiantes interiorizan los conceptos matemáticos. Para mantenerlo relatable, conoce a Maya, una programadora de secundaria que tutoriza a niños más pequeños; a ella le encanta una explicación sencilla respaldada por ejemplos claros y la identificación de patrones.
Maya comienza con una lista rápida. Si un número tiene una forma fraccionaria válida con numerador entero y denominador distinto de cero, es racional. El cero pasa porque su numerador puede ser 0 mientras que su denominador puede ser cualquier entero distinto de cero. La división por cero está prohibida, pero esa regla se refiere al denominador, no al número cero en sí mismo. En clase, esta distinción previene la confusión clásica: 0/5 es válido (y equivale a 0), mientras que 5/0 es indefinido. Esa simple línea ahorra horas de confusión.
Para quienes disfrutan del contexto, el cero también pertenece a otros conjuntos. Es un entero (…−2, −1, 0, 1, 2…), un número entero no negativo (0, 1, 2, 3, …), y un número real (parte del continuo que incluye valores racionales e irracionales). Sin embargo, muchos libros de texto definen los números naturales empezando en 1, lo cual excluye al 0; algunos contextos de informática incluyen el 0 como natural. Saber qué convención usa un curso evita debates innecesarios.
En las aulas de 2025, los profesores utilizan cada vez más IA y explicadores para hacer que estas distinciones sean memorables. Herramientas que ayudan a organizar ejemplos—como tableros de proyectos y planificadores de contenido—reflejan la claridad de las definiciones de fracciones. Para ver cómo las herramientas de pensamiento estructurado están remodelando los flujos de aprendizaje, recursos sobre automatización con APIs o un vistazo a tendencias tecnológicas centradas en educación ilustran cómo escala la claridad. Incluso exploraciones curiosas—como lo que se siente un billón de segundos—pueden contextualizar números grandes y pequeños que aparecen en lecciones sobre fracciones y valor posicional.
- ✅ El cero es racional porque equivale a 0/n con n ≠ 0.
- 🚫 La división por cero (como 5/0) es indefinida, no relacionada con la racionalidad del cero.
- 🧩 El cero pertenece a múltiples conjuntos: enteros, números enteros no negativos y números reales.
- 🧠 Las convenciones varían para los números naturales; verifica la definición de tu curso.
- 🎯 Usa la prueba de fracción: numerador entero y denominador distinto de cero.
| Número 🔢 | ¿Racional? ✅/❌ | Razón 💡 |
|---|---|---|
| 0 | ✅ | Puede escribirse como 0/1, 0/5, … con partes enteras y denominador distinto de cero. |
| 5 | ✅ | Equivale a 5/1 (forma fraccionaria entera). |
| 1/3 | ✅ | Numerador y denominador enteros; decimal es periódico. |
| π | ❌ | No puede expresarse como una razón de enteros; decimal es no periódico. |
| √2 | ❌ | Probado irracional; no hay fracción con enteros que valga √2. |
Insight clave para llevar adelante: la definición fraccionaria por sí sola determina el estado del cero—sin drama, solo estructura.

Cambio de Forma Fraccionaria a Usos Reales del Cero
Antes de pasar a las propiedades, Maya hace una pregunta práctica: ¿dónde aparece el cero fuera de las hojas de trabajo? En presupuestos, una línea con cero significa sin gasto; en código, 0 indica falso o vacío; en tableros de datos, 0 marca la línea base. La misma claridad requerida para tratar 0 como racional ayuda a los equipos a etiquetar, comparar y calcular sin ambigüedades. Para desarrolladores que experimentan con utilidades de tiempo, entender el cero como un offset inicial se alinea con herramientas confiables como recuperación precisa del tiempo en Swift para aritmética de intervalos.
Por Qué el 0 Cumple con la Definición de Número Racional: Fracciones, Decimales y Álgebra
Más allá de la definición formal, la versatilidad del cero como número racional emerge en múltiples representaciones. En cualquier fracción p/q, si p = 0 y q ≠ 0, el valor es 0. Por eso 0/1 = 0/9 = 0/−13 = 0. Cambiar signos o denominador no altera el valor porque multiplicar o dividir cero por cualquier entero distinto de cero sigue dando cero. Esto hace que 0 sea el valor fraccionario más estable frente a transformaciones equivalentes.
Los decimales cuentan la misma historia. Un número racional tiene una expansión decimal finita o periódica. El decimal de cero es 0.0, 0.000…, o cualquier cadena equivalente con ceros finitos o infinitos después del punto—todas son efectivamente terminantes. Si un estudiante ve 0.000, lo clave es que no hay dígitos distintos de cero tras el decimal; así, es racional y equivale a 0.
El álgebra profundiza la intuición. Cero es la identidad aditiva: para cualquier número a, a + 0 = a. Esta identidad encaja bien con las reglas aritméticas racionales. Por ejemplo, sumar 0 a un número racional p/q mantiene a p/q racional. Multiplicar cualquier racional por 0 da 0, que nuevamente es racional. Las propiedades de clausura de los números racionales y el rol especial del 0 se refuerzan mutuamente: nada falla cuando el cero se une al grupo.
Maya muestra una rutina de clase que los estudiantes pueden copiar en notas o tarjetas. La rutina evita atajos y pone sobre la mesa las reglas que realmente importan.
- 🧪 Prueba de fracción: escribe el número como p/q con enteros p, q y q ≠ 0 → racional.
- 🔁 Prueba decimal: terminante o periódico → racional (el decimal de 0 son todos ceros).
- ➕ Revisión identidad: sumar 0 no cambia nada; multiplicar por 0 da 0.
- 🧭 Sanidad de signo: 0/−7 = 0/7 = 0; el signo en el denominador no importa.
- ⚠️ Alerta: denominador 0 hace la expresión indefinida, no “irracional.”
| Representación 🧮 | Ejemplo | ¿Racional? 🔍 | Razón 🧠 |
|---|---|---|---|
| Fracción | 0/19 | ✅ | Numerador entero y denominador distinto de cero → valor 0. |
| Decimal | 0.000… | ✅ | Decimal terminante (o efectivamente terminante). |
| Forma entera | 0 | ✅ | Todo entero es racional (n = n/1). |
| Número mixto | 0 0/5 | ✅ | Equivalente a 0; la parte fraccionaria desaparece. |
| Notación científica | 0.0 × 10³ | ✅ | Sigue siendo 0; la notación no afecta racionalidad. |
Para quienes disfrutan los cruces con tecnología, los coaches de redacción impulsados por IA pueden ayudar a mantener consistencia en explicadores; mira cómo un coach de escritura para claridad o las bibliotecas curadas para salidas estructuradas reflejan la confiabilidad de las reglas fraccionarias. Y si hay que hacer seguimiento durante semanas, utilidades como contadores calendáricos son útiles compañeros.
En resumen: ya sea escrito como fracción, decimal o entero, el cero sigue siendo racional—y esa consistencia es precisamente lo que lo hace tan útil.
Conceptos Erróneos Comunes sobre el Cero: División, Límites y Casos “Complicados”
La confusión más fuerte sobre el cero surge de mezclar reglas diferentes. La trampa clásica es confundir “la división por cero es indefinida” con “el cero no es racional.” No tienen nada que ver entre sí. En la fracción p/q, el único movimiento prohibido es q = 0. Fijar p = 0 está permitido y es inofensivo. Maya usa una analogía rápida: un denominador cero es como pedir asientos en un vuelo que no existe—ningún pase de abordar lo arregla. Pero tener un numerador cero solo significa que no hay pasajeros; el vuelo sí existe.
Los límites crean otro nudo. Considera lim (x→0) 1/x. Al acercarse desde el lado positivo se dispara a +∞; desde el lado negativo, cae a −∞. Esto nos dice algo sobre el comportamiento cerca de cero, no sobre el valor de cero ni su racionalidad. De igual modo, las “formas indeterminadas” como 0/0 aparecen en cálculo al evaluar límites, pero la expresión 0/0 es indefinida como número. Ninguna de estas ideas analíticas revoca la membresía del cero en el conjunto racional.
Otros puntos complicados surgen en combinatoria y álgebra. El factorial 0! es 1 por definición (coherente con recorrencia y lógica de producto vacío), que es racional. La potenciación también puede parecer extraña: 0^0 queda indefinida en muchos contextos porque extensiones competidoras entrarían en contradicción con propiedades deseables; en matemáticas discretas, a veces se toma como 1 para simplificar fórmulas. Independientemente de estas reglas marginales, el valor 0 sigue siendo racional.
- 🧯 Mito: “La división por cero prueba que 0 no es racional.” Realidad: solo los denominadores no pueden ser 0; los numeradores sí.
- 📉 Mito: “Los límites en 0 definen qué ‘es’ el cero.” Realidad: los límites describen comportamiento cercano, no identidad del cero.
- 🧩 Hecho: 0! = 1 → racional; 0^0 depende del contexto pero no afecta la racionalidad del cero.
- 🔄 Hecho: los decimales periódicos indican racionalidad; el decimal del cero es un simple repetido de ceros.
- 🧭 Consejo: mantén las reglas aritméticas, leyes de límites y definiciones de conjuntos en compartimentos mentales separados.
| Expresión/Idea 🧠 | Estado | Impacto en la Racionalidad del Cero 🎯 | Consejo para Estudiantes ✍️ |
|---|---|---|---|
| 5/0 | Indefinido ❌ | Ninguno; no está relacionado con si 0 es racional. | El denominador no puede ser 0. Punto. |
| 0/5 | Válido ✅ | Confirma que 0 es un número racional. | Cualquier denominador distinto de cero funciona. |
| lim (x→0) 1/x | No tiene límite finito | No clasifica al 0; trata el comportamiento cercano a 0. | Separa cálculo de aritmética. |
| 0! | Es 1 | Racional (1/1) ✅ | Convención de producto vacío. |
| 0^0 | Contextual | No cambia el estado del cero | Sigue las reglas de tu curso. |
Cuando los modelos mentales necesitan afilarse, flujos de trabajo bien estructurados ayudan. Artículos para mejorar la disciplina de evaluación, como medir lo que importa en aulas 2025, o para manejar cambios de contexto, como con gestionar ventanas de contexto, muestran cómo definiciones cuidadosas previenen errores de categoría. Categorías claras son justamente lo que mantienen al cero racional y a la división por cero fuera de límites—dos verdades que conviven felizmente.

Puentear a Historia y Axiomas
Los estudiantes a menudo preguntan: si las reglas son tan ordenadas, ¿por qué la humanidad tuvo dificultades para adoptar el cero? Ese es el punto perfecto para contar la historia de los marcadores de posición, los mercaderes y los axiomas que cementaron las definiciones actuales.
De Marcadores de Posición Antiguos a Axiomas Modernos: Cómo el Cero Ganó su Lugar
El camino del cero de “nada” a un número completo no fue inmediato. Los escribas babilonios usaban un símbolo marcador de posición para mantener el valor posicional claro, pero el concepto del cero como número independiente arraigó en India, con matemáticos como Brahmagupta que articulaban la aritmética con cero alrededor del siglo VII. El comercio y la erudición difundieron estas ideas por el mundo islámico y Europa, donde la resistencia se suavizó gradualmente al probar la indispensable notación posicional para comercio y astronomía. El auge del álgebra y luego del cálculo afianzaron la centralidad del cero.
Los enfoques axiomáticos modernos hacen la clasificación a prueba de errores. Partiendo de estructuras como los axiomas de Peano para los números naturales, los matemáticos construyen los enteros a partir de clases de equivalencia de pares de naturales, y los racionales a partir de clases de equivalencia de pares enteros (p, q) con q ≠ 0. En esa construcción, la clase [(0, 1)] representa el número racional 0—claro y sin ambigüedades. Por eso los libros de texto afirman sin titubeos que el cero es racional. La única diferencia está en si los “números naturales” incluyen al cero; cualquiera de las dos opciones es consistente, pero los profesores deben aclarar su convención.
Maya usa una línea de tiempo corta para ayudar a los estudiantes a anclar la evolución. Hace que la definición actual parezca el final de un largo proyecto de ingeniería: las piezas encajan porque fueron diseñadas para eso.
- 📜 Los marcadores de posición en la antigua Babilonia prepararon la notación posicional.
- 🧮 Matemáticos indios formalizaron la aritmética con cero y números negativos.
- 🌍 El intercambio de conocimiento a través del comercio consolidó el 0 en las matemáticas globales.
- 🏛️ Los sistemas axiomáticos derivaron los racionales de enteros con q ≠ 0.
- 🔧 La computación y ciencias de datos estandarizaron el papel del cero en indexación y lógica.
| Era ⏳ | Hito | Impacto sobre la Racionalidad del 0 🎯 | Gancho de Memoria 📌 |
|---|---|---|---|
| Antigua | Surgimiento de marcador | Prepara pensamiento posicional pero aún no es número | “Asiento vacío” en línea numérica |
| India clásica | 0 como número con operaciones | Las reglas aritméticas se estabilizan | 0 × a = 0, a + 0 = a |
| Transmisión medieval | El comercio y la erudición difundieron el valor posicional | La notación se estandariza | Los mercaderes necesitan ceros |
| Axiomas modernos | Construir ℚ desde enteros vía pares (p, q) | [(0, 1)] es 0 racional ✅ | q ≠ 0 es la única restricción |
Los educadores hoy mezclan contexto histórico con herramientas digitales para mejorar la retención. Blogs de aula que exploran historias tecnológicas delicadas—como debates legales vinculados a IA—modelan por qué importan las definiciones precisas. De forma similar, artículos comparando asistentes, como Copilot vs. ChatGPT, reflejan la idea de que reglas consistentes llevan a resultados confiables. Incluso discusiones sobre manejo de datos y análisis de archivos refuerzan la lección: entradas limpias y restricciones claras—como q ≠ 0—mantienen los sistemas estables.
Para los estudiantes: el cero no apareció por arte de magia; fue diseñado en el sistema numérico, y su estatus racional está inscrito en su construcción.
Razonamiento Práctico: Clasificar Números Rápidamente (Con el Cero como Ancla)
Con la visión general lista, Maya lleva a cabo un “clasificador de 90 segundos” para ejercicios. La idea es clasificar cualquier entrada rápidamente verificando forma fraccionaria, comportamiento decimal y pertenencia a conjuntos—usando al cero como caso ancla. El objetivo es rapidez sin descuido. Los estudiantes pueden incluso construir una mini chuleta para los márgenes del examen.
Comienza con la prueba de fracción. ¿Puede ser p/q con enteros p, q y q ≠ 0? Si sí, es racional. Si la forma decimal termina o es periódica (como 0.125 o 0.333…), es racional. Si ni termina ni es periódica (como π o √2 como decimales), es irracional. Para enteros, recuerda que n = n/1 hace todo entero racional; por eso 0 es racional porque 0 = 0/1. Estas pruebas aplican uniformemente en ejercicios.
- 🧩 Paso 1: Intenta p/q con partes enteras; rechaza q = 0 inmediatamente.
- 🔎 Paso 2: Inspecciona decimales: terminante o periódico → racional.
- 🧱 Paso 3: Enteros califican automáticamente (n = n/1), incluyendo 0.
- 🛑 Paso 4: Si ninguno aplica y los decimales no repiten → irracional.
- 🗂️ Paso 5: Toma nota de pertenencia a conjuntos (enteros no negativos, enteros, reales) para crédito completo.
| Valor 🔢 | Forma Fraccionaria | ¿Racional? ✅/❌ | Etiquetas de Conjunto 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | Entero, No Negativo, Real |
| −3/4 | −3/4 | ✅ | Racional, Real |
| 0.125 | 1/8 | ✅ | Racional, Real |
| 0.333… | 1/3 | ✅ | Racional, Real |
| √2 | — | ❌ | Irracional, Real |
| π | — | ❌ | Irracional, Real |
¿Quieres refuerzo audiovisual? Un video explicativo rápido puede fijar la frontera racional vs. irracional mientras mantiene al cero en primer plano. Para profesores creando listas de reproducción, consultas estructuradas pueden ayudar a encontrar clips concisos.
Los estudiantes con inclinación tecnológica suelen prototipar sistemas de notas y pipelines; si es tu estilo, flujos modulares como servidores de medios virtualizados pueden hospedar recursos de estudio, y la automatización de tareas vía herramientas API puede generar automáticamente conjuntos de práctica focalizados en casos límite como 0, 0/0 (indefinido) y 1/0 (indefinido). Un pipeline limpio refuerza una definición limpia.
Reflexión final para esta sección: la consistencia gana. El cero se comporta igual en todas las representaciones, haciéndolo el ancla perfecta para el clasificador.
Aplicaciones Periféricas: Valor Posicional, Sistemas de Datos y Narrativas en el Aula Donde el Cero Importa
La racionalidad del cero no es solo una demostración; sustenta cómo se comportan los sistemas de información y los planes de estudio. En el valor posicional en base diez, un dígito 0 indica “ninguno en esta posición,” lo que mantiene correcta la magnitud: 101 difiere de 11 porque el 0 del medio preserva el lugar de las decenas como vacío. En hojas de cálculo y código, un cero suele indicar “sin ítems,” “sin error,” o línea base—haciendo cálculos determinísticos. Un tratamiento desordenado del 0 introduciría caos en tableros, matemáticas del tiempo y algoritmos.
Considera tareas de clasificación de datos: si una columna debe almacenar solo números racionales, el cero debe admitirse, o las medidas legítimas en la línea base serían rechazadas. Maya diseña una pequeña demo de “higiene de datos”: alimenta un parser con mezcla de enteros, fracciones simples, decimales periódicos y conocidos irracionales; el validador acepta cualquier cosa convertible a p/q con q ≠ 0. La demo registra al 0 como válido en las vías enteras y fraccionarias. Desde ahí, los estudiantes escriben pruebas unitarias para confirmar clausura bajo suma y multiplicación con cero.
- 🧮 Valor posicional: 0 mantiene dígitos alineados, evitando errores de magnitud.
- 🧰 Integridad de datos: el cero debe validar en campos solo racionales.
- 🧷 Manejo de errores: los errores 1/0 se capturan en análisis, no en tiempo de ejecución.
- 🧪 Pruebas: incluye 0 en todas las pruebas de propiedad de clausura para racionales.
- 📚 Narrativa: Maya etiqueta 0 como “el ancla” en rúbricas y documentos de proyecto.
| Escenario 🗂️ | Rol del Cero | Por Qué la Racionalidad Ayuda 🎓 | Pista en Clase 🛎️ |
|---|---|---|---|
| Valor posicional | Sostiene posiciones vacías | Interpretación consistente de magnitud | “0 mantiene el asiento caliente” 😊 |
| Validación | Aceptado como 0/1 | Restricciones limpias en entrada | Prueba 0, 1/0, 0/0 por separado |
| Cálculo | Identidad aditiva | Simplifica demostraciones y código | Usa 0 en pruebas unitarias |
| Enseñanza | Caso ancla | Reduce la difusión de conceptos erróneos | Empieza ejemplos con 0 |
Break de curiosidad: la comunicación sobre matemáticas se beneficia del lenguaje y contexto precisos. Incluso fuera de matemáticas, la claridad importa—ya sea al analizar significados de emojis para el tono en foros estudiantiles, evaluar tecnologías para seguridad escolar, o detectar narrativas noticiosas. La lección se transfiere: definiciones, restricciones y ejemplos previenen confusión. De igual forma, un agujero de conejo inocente como interpretación de símbolos recuerda a los estudiantes lo rápido que el significado puede desviarse sin reglas compartidas—justamente por eso la definición racional mantiene al cero firme.
Conclusión para este segmento: la racionalidad del cero es más que una etiqueta; es una garantía de que los sistemas—desde la aritmética hasta el análisis—se mantengan predecibles.
Práctica Extra con el Mini-Conjunto de Maya
Los estudiantes de Maya clasifican estos en menos de un minuto: 0, −7, 2/9, 0/3, 3/0, 0.1010010001…, y √9. Los aciertos: 0 (racional), −7 (racional), 2/9 (racional), 0/3 (racional), 3/0 (indefinido), 0.1010010001… (no periódico, no terminante → probablemente irracional), √9 (igual a 3 → racional). La habilidad para identificar patrones se transfiere entre unidades y exámenes.
{“@context”:”https://schema.org”,”@type”:”FAQPage”,”mainEntity”:[{“@type”:”Question”,”name”:”¿Se considera el cero un número racional?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Sí. Por definición, un número racional es cualquier valor expresable como p/q con enteros p y q y q ≠ 0. El cero encaja porque 0 = 0/1, 0/5, o 0/n para cualquier entero distinto de cero n.”}},{“@type”:”Question”,”name”:”¿La división por cero hace que el cero no sea racional?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”No. La división por cero es una regla sobre denominadores, no sobre el número cero. 5/0 y 0/0 son expresiones indefinidas, pero el 0 en sí mismo sigue siendo un número racional válido.”}},{“@type”:”Question”,”name”:”¿Es el cero un número entero, entero no negativo o natural?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”El cero es un entero y un número entero no negativo. Si es un número natural depende de la convención: muchos cursos comienzan los naturales en 1, mientras que algunos contextos incluyen el 0.”}},{“@type”:”Question”,”name”:”¿El cero puede escribirse como decimal y seguir siendo racional?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Sí. La forma decimal del cero es 0.0 (o 0.000…), que es terminante. Los decimales terminantes y periódicos son racionales por definición.”}},{“@type”:”Question”,”name”:”¿Cómo ayuda el papel del cero en álgebra?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”El cero es la identidad aditiva: a + 0 = a. Mantiene las ecuaciones balanceadas y simplifica demostraciones. Multiplicar cualquier número racional por 0 da 0, que es racional.”}}]}¿Se considera el cero un número racional?
Sí. Por definición, un número racional es cualquier valor expresable como p/q con enteros p y q y q ≠ 0. El cero encaja porque 0 = 0/1, 0/5, o 0/n para cualquier entero distinto de cero n.
¿La división por cero hace que el cero no sea racional?
No. La división por cero es una regla sobre denominadores, no sobre el número cero. 5/0 y 0/0 son expresiones indefinidas, pero el 0 en sí mismo sigue siendo un número racional válido.
¿Es el cero un número entero, entero no negativo o natural?
El cero es un entero y un número entero no negativo. Si es un número natural depende de la convención: muchos cursos comienzan los naturales en 1, mientras que algunos contextos incluyen el 0.
¿El cero puede escribirse como decimal y seguir siendo racional?
Sí. La forma decimal del cero es 0.0 (o 0.000…), que es terminante. Los decimales terminantes y periódicos son racionales por definición.
¿Cómo ayuda el papel del cero en álgebra?
El cero es la identidad aditiva: a + 0 = a. Mantiene las ecuaciones balanceadas y simplifica demostraciones. Multiplicar cualquier número racional por 0 da 0, que es racional.

-

 Tecnologia1 day ago
Tecnologia1 day agoSu tarjeta no admite este tipo de compra: qué significa y cómo solucionarlo
-

 Modelos de IA1 day ago
Modelos de IA1 day agoOpenAI vs Tsinghua: Elegir entre ChatGPT y ChatGLM para tus necesidades de IA en 2025
-

 Internet23 hours ago
Internet23 hours agoExplorando el Futuro: Lo Que Necesita Saber Sobre Internet-Enabled ChatGPT en 2025
-

 Modelos de IA1 day ago
Modelos de IA1 day agoElegir tu compañero de investigación en IA en 2025: OpenAI vs. Phind
-

 Tecnologia10 hours ago
Tecnologia10 hours agoComprendiendo la degeneración dura: qué significa y por qué importa en 2025
-

 Gaming18 hours ago
Gaming18 hours agoGratis para todos pelea nyt: estrategias para dominar la batalla definitiva