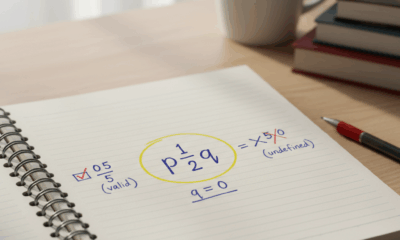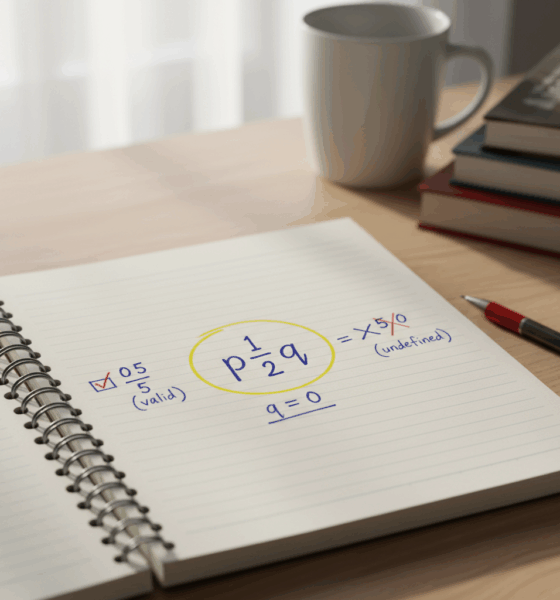
సాంకేతికత
సున్నా ఒక తర్కసంబంధ సంఖ్యగా పరిగణించబడతాఉందా? సులభంగా వివరించినది
శూన్యం రేషనల్ సంఖ్యగా పరిగణించబడుతుందా? సులభమైన వివరణ
భాగాల సమస్యలతో పుంజుకోవడంలో ఉన్న విద్యార్థిని అడగండి: శూన్యం ఒక రేషనల్ సంఖ్యా? గణితంలో స్పష్టమైన సమాధానం అవును. రేషనల్ సంఖ్య అంటే p/q రూపంలో వ్రాయగలిగిన ఏదైనా విలువ, ఇక్కడ p మరియు q పరిమిత సంఖ్యలు (ఇంటీజర్లు), మరియు హ్రాసకం q సున్నా కాకూడదు. ఎందుకంటే 0 ను 0/1, 0/7 లేదా సాధారణంగా ఏ సున్నా కాని పరిమిత సంఖ్య n కోసం 0/n గా వ్యక్తపరచవచ్చు, కాబట్టి ఇది అర్థం అవుతుంది. కానీ సంఖ్య సిద్ధాంతం, పరిమితులు (limits) మరియు విద్యార్థులు గణిత సంకల్పాలను ఎలా గ్రహిస్తారనే దృక్కోణాలు విస్తరిస్తే విషయం మరింత లోతైనదవుతుంది. సంబంధం కల్పించేందుకు, విజయవంతంగా చిన్న పిల్లలకి ఉపధ్యాయుగా ఉన్న హైస్కూల్ కోడర్ మాయా పరిచయం చేసుకుందాం; ఆమెకు చక్కని స్వచ్ఛమైన ఉదాహరణలు మరియు నమూనాల కనుగొనడం వైపు ప్రాముఖ్యత ఉంది.
మాయా తక్కువ సమయంలో ఒక చెక్లిస్ట్ ఇచ్చి ప్రారంభిస్తుంది. ఒక సంఖ్య సరైన భాగ రూపంలో ఉంటే, అందులో పరిమిత పూర్తి భాగం మరియు సున్నా కాని హ్రాసకం ఉంటే అది రేషనల్. శూన్యం పాస్ అవుతుంది ఎందుకంటే దాని పూర్తి భాగం 0 అవుతుంది, హ్రాసకం ఏ సున్నా కాని పరిమిత సంఖ్య కావచ్చు. సున్నాతో భాగాకరణ చేయడం నిషిద్ధమే, కానీ ఆ నియమం హ్రాసకం మీదే వర్తించేది, శూన్యంకు కాదు. తరగతిలో, ఈ తేడా క్లాస్లో సాధారణంగా కలగింతలను నివారిస్తుంది: 0/5 సరైనది (మరియు 0 కు సమానం), 5/0 నిర్వచన రహితమైనది. ఆ ఒక పంక్తి సమయం చాలా గందరగోళాన్ని తడుతుంది.
పరిస్థితులు ఇష్టపడే విద్యార్థుల కోసం, శూన్యం ఇతర సెట్లలో కూడా ఉంటుంది. ఇది ఒక పరిమిత సంఖ్య (…−2, −1, 0, 1, 2…), ఒక పూర్తి సంఖ్య (0, 1, 2, 3, …), మరియు ఒక వాస్తవ సంఖ్య (రేషనల్ మరియు ఇరేషనల్ విలువల మధ్య మొత్తం నిరంతరం). అయితే, చాలా పాఠ్యపుస్తకాలు స్వభావిక సంఖ్యలు 1 నుండి ప్రారంభమవుతాయని నిర్వచిస్తాయి, కాబట్టి 0 తప్పదిగా ఉంటుంది; కొంత కంప్యూటర్ సైన్స్ సందర్భాల్లో 0 ను స్వభావిక సంఖ్యగా పరిగణిస్తారు. ఈ గమనిక ఏ సంప్రదాయాన్ని కోర్సు అనుసరిస్తుందో తెలుసుకోవడం అనవసర వాదనలను నివారిస్తుంది.
2025 తరగతుల్లో, శిక్షకులు మరింతగా AI మరియు వివరణకర్తలను ఉపయోగించి ఈ భేదాలను గుర్తుంచుకునేలా చేస్తారు. ప్రాజెక్ట్ బోర్డులు మరియు కంటెంట్ ప్లానర్ల లాంటి పరికరాలు ఉదాహరణలను సమన్వయ పరుస్తూ భాగాల నిర్వచనం వివేకాన్ని ప్రతిబిమ్బిస్తాయి. నిర్మిత ఆలోచనా పరికరాలు ఎలా విద్యా కార్యకలాపాలను మార్చుతున్నాయో చూడాలంటే, APIలతో ఆటోమేషన్ పై వనరులు లేదా విద్యా కేంద్రిత సాంకేతిక ధోరణులు పరిశీలించండి. విభిన్న, కొంత విపరీతమైన పరిశోధనలు కూడా ఉన్నాయి — ఉదా: ఒక బిలియన్ సెకన్ల అనుభూతి వంటి — ఇవి భాగాలు మరియు స్థానం విలువ పాఠాలలో పెద్ద మరియు చిన్న సంఖ్యలకు సందర్భం ఇస్తాయి.
- ✅ శూన్యం రేషనల్ ఎందుకంటే అది 0/n కి సమానం, n ≠ 0.
- 🚫 సున్నాతో భాగాకరణ (ఉదా: 5/0) నిర్వచన రహితంగా ఉంటుంది, ఇది శూన్య రేషనలిటీకి సంబంధం లేదు.
- 🧩 శూన్యం పలు సెట్ల భాగం: పరిమిత, పూర్తీ, వాస్తవ సంఖ్యలు.
- 🧠 స్వభావిక సంఖ్యల కోసం సంప్రదాయాలు మారుతుంటాయి; మీ కోర్సు నిర్వచనాన్ని తనిఖీ చేయండి.
- 🎯 భాగ పరీక్ష ఉపయోగించండి: పరిమిత పూర్తి భాగం మరియు సున్నా కాని హ్రాసకం.
| సంఖ్య 🔢 | రేషనల్? ✅/❌ | కారణం 💡 |
|---|---|---|
| 0 | ✅ | 0/1, 0/5, … లాగా integer భాగాలతో మరియు సున్నా కాని హ్రాసకం. |
| 5 | ✅ | 5/1 (పరిమిత భిన్న రూపం)తో సమానం. |
| 1/3 | ✅ | ఇంటిజర్ పూర్తి భాగం మరియు హ్రాసకం; దశాంశం తిరుగుతుంటుంది. |
| π | ❌ | ఇంటిజర్ల నిష్పత్తిగా తెలియదు; దశాంశం తిరగని. |
| √2 | ❌ | అసంగతమైనది; √2కు సమానం ఐనా integer fraction లేదు. |
ముఖ్యమైన అర్థం పంచుకోదలుచుకోండి: భాగ నిర్వచనం మాత్రమే శూన్యం స్థితిని నిర్ణయిస్తుంది—విషాదం లేదు, కేవలం నిర్మాణం.

భాగ రూపం నుండి జీవితంలో శూన్యం ఉపయోగాల దిశలో
గుణాత్మక లక్షణాలకు దగ్గరగా వెళ్లే ముందు, మాయా ఒక ప్రాక్టికల్ ప్రశ్న అడుగుతుంది: తరగతి పత్రాల బయట శూన్యం ఎక్కడ కనిపిస్తుందో? బడ్జెట్లలో, శూన్యం లైన్ అంటే ఖర్చు లేదు; కోడులో, 0 తప్పు లేదా ఖాళీ సూచిస్తుంది; డేటా డ్యాష్బోర్డుల్లో, 0 ప్రాథమిక స్థితిని సూచిస్తుంది. 0 ను రేషనల్గా భావించాల్సిన స్పష్టత, జట్లు లేబుల్ చేయడంలో, పోల్చడంలో మరియు లెక్కింపు లో తలపిస్తున్న అపార్థాలను నివారిస్తుంది. సమయ ఉపయోగాలను ప్రయోగం చేస్తున్న అభివృద్ధి దారులు, 0 ను ప్రారంభ అంతరంగా గ్రహించడం విశ్వసనీయ పరికరాలుగా Swift-లో సమయ సঠితిని పొందడం వంటి పనులతో అనుసరిస్తారు.
0 రేషనల్ సంఖ్య నిర్వచనానికి ఎలా సరిపోతుంది: భాగాలు, దశాంశాలు మరియు బీజగణితం
ప్రమాణిక నిర్వచనం తోపాటు, ఒక రేషనల్ సంఖ్యగా శూన్యం యొక్క బహుళ రూపాలు వెలుగులోకి వస్తాయి. ఏ పాక్షికంలో p/q, p = 0 మరియు q ≠ 0 అయితే, అది 0. అందుకే 0/1 = 0/9 = 0/−13 = 0. సైన్లని మార్చినా లేదా హ్రాసకం మారినా విలువ మార్చదు, ఎందుకంటే 0 ను ఏ సున్నా కాని integer తో గుణిస్తే లేదా భాగిస్తే 0 మాత్రమే వస్తుంది. ఇది 0 ను సమాన మార్పిడి కింద అత్యంత స్థిరమైన భాగ విలువగా చేస్తుంది.
దశాంశాలు కూడా అదే కథ చెబుతాయి. రేషనల్ సంఖ్య ఓ ముగిసే లేదా తిరిగే దశాంశ విస్తరణ కలిగి ఉంటుంది. శూన్యం యొక్క దశాంశం 0.0, 0.000… లేదా అనంతసారాలున్నా లేదా ఉన్నా అంతిమంగా వేరేవి లేని 0 సిరీస్—ఇది ప్రతీ ఎంపిక తగినంతగా ముగియుటగా పరిగణించబడుతుంది. విద్యార్థి 0.000 ను చూసినపుడు, దశాం తర్వాత ఏ ఎలాంటి సున్నా కాని అంకెలు లేవంటూ తెలుసుకోవడం ముఖ్యము; కాబట్టి అది రేషనల్, మరియు 0 కు సమానం.
బీజగణితం సూత్రీకరణను మరింత అర్థం చేసుకుంటుంది. 0 అనేది సమాపక పరిమాణము: ఏ సంఖ్య a కోసం అయినా a + 0 = a. ఈ లక్షణం రేషనల్ గణిత నియమాలతో బాగా జతకట్టుకుపోయింది. ఉదాహరణకు, 0 ని రేషనల్ సంఖ్య p/q కి యోడిస్తే అది ఇంకా రేషనల్గా ఉంటుంది. ఏ రేషనల్ ని 0 తో గుణిస్తే 0 వస్తుంది, ఇది మళ్ళీ రేషనల్. రేషనల్ సంఖ్యల మూసి లక్షణాలు మరియు 0 యొక్క ప్రత్యేక పాత్ర ఒకరినొకరు బలపరుస్తాయి: 0 పార్టీలో చేరినప్పటికీ ఏది కూడా తప్పదు.
మాయా తరగతిలో learners తమ గమనికలు లేదా ఫ్లాష్కార్డుల్లో ప్రతిరూపించుకునే అలవాటును చూపిస్తుంది. ఈ అలవాటు చిన్నవేళ షార్ట్కట్స్ వద్దు మరియు నిజానికి ముఖ్యమైన నియమాలను ప్రకటిస్తుంది.
- 🧪 భాగ పరీక్ష: సంఖ్యను p/q (పరిమితలు p, q , q ≠ 0) రూపంలో వ్రాయండి → రేషనల్.
- 🔁 దశాంశ పరీక్ష: ముగిసే లేదా తిరిగే → రేషనల్ (0 యొక్క దశాంశం శూన్యాలన్నీ).
- ➕ గుర్తింపు చెక్: 0 యోడించడం అర్థం మార్చదు; 0 తో గుణించడం 0.
- 🧭 సైన్ సమాధానం: 0/−7 = 0/7 = 0; హ్రాసకం లో సైన్ పనికిరాదు.
- ⚠️ హెచ్చరిక: 0 హ్రాసకం అమలు చేస్తే నిర్వచన రహితం, “అసంగతం” కాదు.
| ప్రతినిధి రూపం 🧮 | ఉదాహరణ | రేషనల్? 🔍 | కారణాలు 🧠 |
|---|---|---|---|
| భాగం | 0/19 | ✅ | పరిమిత పూర్తి భాగం మరియు సున్నా కాని హ్రాసకం → విలువ 0. |
| దశాంశం | 0.000… | ✅ | ముగిసేది (లేదా ప్రభావవంతంగా ముగిసేది) దశాంశ రూపం. |
| పరిమిత రూపం | 0 | ✅ | ప్రతి integer రేషనల్ (n = n/1). |
| మిశ్రమ సంఖ్య | 0 0/5 | ✅ | 0 కు సమానం; భాగ భాగం అస్తవ్యస్తమవుతుంది. |
| శాస్త్రీయ సూత్రీకరణ | 0.0 × 10³ | ✅ | ఇంకా 0; సూత్రీకరణ రేషనలిటీపై ప్రభావం లేదు. |
টెక్కు ఆసక్తి ఉన్న విద్యార్థులు AI ఆధారిత డ్రాఫ్ట్ కోచ్లను ఉపయోగించి వివరణలను సజావుగా ఉంచవచ్చు; స్పష్టత కోసం రచనా కోచ్ లేదా నిర్మిత అవుట్పుట్ల కోసం లైబ్రరీలు రేషనల్ నియమాల విశ్వసనీయతను ప్రతిబింబిస్తాయి. మరియు పురోగతి సరళంగా నమోదు చేయాల్సిన అవసరం ఉంటే, కాలెండర్ ఆధారిత కౌంటర్స్ బాగా సహాయకులు.
మొత్తం విషయం: ఇది భాగం, దశాంశం లేదా పరిమిత రూపంలో వ్రాయబడి ఉన్నా శూన్యం రేషనల్గా మిగిలి ఉంటుంది—ఆ సుస్పష్టతే దీన్ని చాలా ఉపయోగకరంగా చేస్తుంది.
శూన్యం గురించి సామాన్య భ్రమలు: భాగాకరణ, పరిమితులు, మరియు “సంక్లిష్ట” కేసులు
శూన్యం చుట్టూ గల అత్యంత స్పష్టమైన గందరగోళం వేరు అయిన నియమాలు కలగిపోయే దగ్గర నుంచి వస్తోంది. సాధారణ తప్పిదం “సున్నాతో భాగాకరణ నిర్వచన రహితం” మరియు “శూన్యం రేషనల్ కాదు” ఎలాంటి సంబంధం లేని వాటినిని కలగబరుస్తుంది. p/q రూపంలో, q = 0 అనేది మాత్రమే నిషిద్ధం. p = 0 అనేది అనుమతించబడింది మరియు ప్రయోజనకరం. మాయా ఒక సాదా ఉపమానాన్ని ఉపయోగిస్తుంది: 0 హ్రాసకం ఉన్న ఫ్రాక్షన్ అనేది ఉన్న విమానం లేని సీట్ల కోసం అడగడం లాంటిది—బోర్డింగ్ పాస్ ఉపయోగపడదు. కానీ పూర్తి భాగం 0 ఉండటం అంటే ఎవరూ ఆ ప్రయాణానికి రాలేదంటే, విమానం ఇంకా ఉంటుంది.
పరిమితులు తదుపరి గాలింపు. లిమిట్ (x→0) 1/x ను పరిగణించండి. ధనాత్మక వైపు నుంచి దగ్గరగా వస్తే +∞ కు అగలిపోతుంది; ప్రతికూల వైపు నుండి వస్తే −∞ కు పడిపోతుంది. ఇది శూన్యం విలువ లేదా దాని రేషనలిటి గురించినది కాకుండా భవిష్యత్తులో ప్రవర్తన గురించి చెబుతుంది. అదేవిధంగా, కాలికలుస్లో 0/0 అగ్రథిలు (indeterminate forms) కనిపిస్తాయి, కానీ 0/0 ను సంఖ్యగా నిర్వచించలేం. ఈ విశ్లేషణాత్మక ఆలోచనలు కూడా శూన్యం రేషనల్ సెట్ సభ్యత్వాన్ని తొలగించవు.
ఇంకా కొంత సంక్లిష్టమైన విషయాలు కలిగినవి ఉన్నవి, ముఖ్యంగా కలయికశాస్త్రం మరియు బీజగణితంలో. फैक्टोरियल0! నిర్వచన ప్రకారం 1 కు సమానం (పునరావృత మరియు ఖాళీ గుణన లాజిక్తో అనుగుణంగా), ఇది రేషనల్. పరిణామం 0^0 అనేక సందర్భాల్లో నిర్వచన రహితం, ఎందుకంటే విరుద్ధమైన గుణాలు వస్తాయని భావిస్తారు; విడిపడిన గణితంలో కొన్ని సార్లు దీనిని సూత్రీకరణ సరళత కోసం 1 గా పరిగణిస్తారు. ఈ సరిహద్దు నియమాలు వుండగా కూడా, విలువ 0 రేషనల్గా కొనసాగుతుంది.
- 🧯 భ్రమ: “శూన్యాన్ని రేషనల్ కానిది చేస్తేది సున్నాతో భాగాకరణ.” వాస్తవం: కేవలం హ్రాసకాలు 0 కావ తప్పవు; పూర్తి భాగాలు అవుతున్నాయి.
- 📉 భ్రమ: “పరిమితులు 0 వద్ద శూన్యాన్ని నిర్వచిస్తాయి.” వాస్తవం: పరిమితులు పక్కను ప్రవర్తన విశదపరుస్తాయి, శూన్యం స్వరూపం కాదు.
- 🧩 వాస్తవం: 0! = 1 → రేషనల్; 0^0 సందర్భప్రధానంగా ఉంటుంది కానీ శూన్యం రేషనలిటిని మించి ప్రభావం లేదు.
- 🔄 వాస్తవం: తిరిగే దశాంశాలు రేషనల్ సూచిస్తాయి; శూన్యం దశాంశం సున్నాల సాదారణ పునరావృతం.
- 🧭 ప్రొ టిప్: గణిత నియమాలు, పరిమితులు మరియు సెట్ నిర్వచనాలను వేర్వేరుగా మానసిక కంటైనర్లలో ఉంచండి.
| వ్యక్తీకరణ/సంకల్పన 🧠 | స్థితి | శూన్యం రేషనలిటీపై ప్రభావం 🎯 | విద్యార్థి సూచన ✍️ |
|---|---|---|---|
| 5/0 | నిర్వచన రహితం ❌ | ఏదీ కాదు; శూన్యం రేషనల్ అవుతుందో లేదో సంబంధం లేదు. | హ్రాసకం 0 కాకూడదు. పూర్తిగా. |
| 0/5 | సరైనది ✅ | శూన్యాన్ని రేషనల్ సంఖ్యగా నిర్ధారిస్తుంది. | ఏ సున్నా కాని హ్రాసకం పనిచేస్తుంది. |
| lim (x→0) 1/x | అపరిమిత పరిమితి లేదు | 0 ను తరగతి చేయడం లేదు; 0 సమీప ప్రవర్తన గురించి. | క్యాల్క్యులస్ ను గణితశాస్త్రం నుండి వేరు చేయండి. |
| 0! | 1 కు సమానం | రేషనల్ (1/1) ✅ | ఖాళీ గుణకం నియమం. |
| 0^0 | సందర్భ ఆధారితం | శూన్యం స్థితి మార్చదు | మీ కోర్సు నియమాలు అనుసరించండి. |
మానసిక నమూనాలు ముద్రపాఠం కావాలంటే, బాగా నిర్మిత వర్క్ఫ్లో మంచి సహాయం. 2025 తరగతులలో అమ్మకపు పరిస్థితులను మెరుగుపర్చడం లేదా సందర్భ మార్పులను నిర్వహించడం వంటి వ్యాసాలు నిర్వచనాలను కచ్చితంగా ఉంచడం మరియు శ్రేణి పొడిచిపోకుండా నివారించగలిగే విధానాలు ఎలా ఉంటాయో చూపిస్తాయి. స్పష్టమైన వర్గీకరణలు శూన్యాన్ని రేషనల్గా ఉంచుతాయి మరియు సున్నాతో భాగకం చేయడాన్ని నిషిద్ధం చేస్తాయి — ఇరు నిజాలు శాంతియుతంగా కలిసిలేవీ.

చరిత్ర మరియు న్యాయసూత్రాలకు మోస్తరు
విద్యార్థులు తరచుగా అడుగుతారు: ఈ నియమాలు అంత సుసంపన్నమైనవైతే, మానవాళికి శూన్యం స్వీకరించడంలో సమస్య ఎందుకు వచ్చింది? ఇది స్థానచిహ్నాల, వ్యాపారులు, మరియు ఆధునిక నిర్వచనాలను స్థిర పరిచే సూత్రాల కథకు సరైన ప్రవేశం.
ప్రాచీన స్థాన చిహ్నాల నుండి ఆధునిక న్యాయసూత్రాలు వరకు: శూన్యం స్థానం పొందిన విధానం
“ఏమీ లేదు” నుండి పూర్తి సంఖ్యగా మారటం శూన్యానికి తక్షణం కాదు. బేబిలోనియన్ గ్రంథరచయితలు స్థాన విలువ క్రమాన్ని సరిగ్గా ఉంచడానికి స్థాన చిహ్నాన్ని ఉపయోగించారు, కానీ శూన్యం కనిపెట్టబడినప్పుడు అది స్వతంత్ర సంఖ్యగా భారతదేశంలో, 7వ శతాబ్దంలో బ్రహ్మగుప్తుడు లాంటి గణిత శాస్త్రవేత్తలు ఇందులో అంకెల గణితం గురించి ప్రకటించారు. వాణిజ్యం మరియు విద్యాశాఖ ఈ ఆలోచనలను ఇస్లామిక్ ప్రపంచం ద్వారా యూరోప్కు తీసుకువెళ్లి, స్థానం గుర్తుచేసే విలువ వ్యాపారంలో, ఖగోళ శాస్త్రంలో ముఖ్యత పొందడంతో ప్రతిఘటన మారం అయ్యింది. బీజగణితం మరియు తర్వాత కాలికలస్ ల యొక్క ఎదుగుదల శూన్యం ప్రధానతను నిర్ధారించారు.
ఆధునిక సూత్రాత్మక విధానాలు వర్గీకరణను బలంగా నిలుపుతాయి. స్వభావిక సంఖ్యల కోసం పడిన పియానో సూత్రాలు మొదలుకుని, గణిత శాస్త్రవేత్తలు పరిమిత సంయుక్తాల నుండి పరిమిత సంఖ్యలను, integer జతల సారూప్యత తరగతుల నుండి rationals ను q ≠ 0 ఉండే integer జతల నుండి గాఢంగా (p, q) నిర్మించారు. ఆ నిర్మాణంలో, [(0, 1)] రేషనల్ సంఖ్య 0 అంటే స్పష్టమైన మరియు సంకోచ రహితమైనగా ఉంటుంది. అటువంటి కారణంతో పాఠ్యపుస్తకాలు సంకోచం లేకుండా శూన్యం రేషనల్ అని చెబుతాయి. ఒప్పందంలో ఏ తప్పలేదు కాబట్టి “స్వభావిక సంఖ్యలు” 0 ను కలిగిస్తాయా అన్నది; రెండూ కారణాలు సुसంపన్నంగా ఉన్నాయి, కాని ఉపాధ్యాయులు తమ నియమాన్ని ప్రకటించాలి.
మాయా ఒక చిన్న కాలక్రమాన్ని ఉపయోగించి విద్యార్థులకు కలిసిపోయిన మార్గాన్ని చూపిస్తుంది. ఇది నేటిదిన నిర్వచనాన్ని ఇంజనీరింగ్ ప్రాజెక్టు ముగింపు లాగా గ్రహింపజేస్తుంది: భాగాలు కలిసి డిజైన్ అవుతాయని.
- 📜 ప్రాచీన బేబిలోనులో స్థాన సూచికలు స్థాన విలువకు రంగురంగుల వాయిదं నిదర్శనం.
- 🧮 భారత గణిత శాస్త్రవేత్తలు శూన్యం మరియు ऋణાંકాలతో గణితాన్ని సూత్రీకరించారు.
- 🌍 వ్యాపారం ద్వారా జ్ఞానం బదిలీ 0 ను అంతర్జాతీయ గణితంలో మరింత బలపరిచింది.
- 🏛️ న్యాయసూత్రాలు integer జతల ద్వారా rationals నిర్మాణం q ≠ 0 తో చెప్పారు.
- 🔧 కంప్యూటింగ్ మరియు డేటా శాస్త్రం 0 పాత్రను సూచికలతో మరియు లాజిక్ లో స్థిరపరిచింది.
| కాలం ⏳ | దశ | 0 యొక్క రేషనలిటీ మీద ప్రభావం 🎯 | జ్ఞాపక సూచన 📌 |
|---|---|---|---|
| ప్రాచీన | స్థాన సూచిక | స్థాన చింతనకు తగినదిగా, సంఖ్యగా కాదు | సంఖ్యల రేఖలో “ఖాళీ సీటు” |
| క్లాసికల్ ఇండియా | 0 ఒక ఆపరేషన్ తో సంఖ్యగా | గణిత నియమాలు స్థిరపడ్డాయి | 0 × a = 0, a + 0 = a |
| మధ్య యుగంలో బదిలీ | వ్యాపారం మరియు శాస్త్రవేత్తలతో స్థాన విలువ వ్యాప్తి | సూత్రీకరణ స్థిరమైంది | వ్యాపారులకు నెమ్మదిగా తెలిసింది |
| ఆధునిక న్యాయసూత్రాలు | పరిమితాలను integer ల నుండి జతల ద్వారా నిర్మించారు (p, q) తో q ≠ 0 | [(0, 1)] రేషనల్ 0 ✅ | q ≠ 0 మాత్రమే నిషేధం |
ఈ రోజుల్లో శిక్షకులు చరిత్రకాక్ష్యాలతో కలిసి డిజిటల్ సాధనాలను ఉపయోగించి జ్ఞాపకం పెంచుతారు. సున్నితమైన సాంకేతిక కథలను విపరిచే తరగతి బ్లాగులు — ఉదా: AIతో సంబంధిత చట్ట పర్యవేక్షణ — కచ్చితమైన నిర్వచనాల ప్రాముఖ్యతను సూచిస్తాయి. అలాగే సహాయక比较లు, కోపీ లోట్ Vs. చాట్ GPT వంటి అవగాహనలు సూటి నియమాలపై విశ్వసనీయ ఫలితాలకు దారి చూపుతాయి. డేటా నిర్వహణా, గైలు సంభాషణలు మరియు ఫైల్ విశ్లేషణ ఈ పాఠాన్ని పునరుద్దేశిస్తాయి: స్వచ్ఛమైన ఇన్పుట్లు మరియు స్పష్టమైన పరిమితులు — q ≠ 0 లాంటివి — వ్యవస్థలను స్థిరంగా ఉంచుతాయి.
విద్యార్థులకు తీసుకోవాల్సిన పాఠం: శూన్యం తక్షణం కనిపించలేదు; అది సంఖ్యావ్యవస్థలో ఇంజనీరింగ్ ద్వారా సంకలనం అయింది మరియు దాని రేషనల్ స్థితి నిర్మాణంలోనే ఉన్నాయి.
ప్రాక్టికల్ ఆలోచన: నెంబర్లను త్వరగా వర్గీకరించడం (శూన్యం అంకంగా)
వिस्तృత దృశ్యం సెట్ చేసిన తరువాత, మాయా “90 సెకన్ల సార్టర్” ని అమలు చేస్తుంది. ఆలోచన ఏ ఇన్పుట్ అయినా వేగంగా వర్గీకరించడానికి భాగ రూపం, దశాంశ ప్రవర్తన మరియు సెట్ సభ్యత్వాన్ని తనిఖీ చేయడం—శూన్యాన్ని అంకగా ఉపయోగించడం. లక్ష్యం వేగంగా కానీ జాగ్రత్తగా ఉండటం. విద్యార్థులు పరీక్ష పక్కన చిన్న చీట్షీట్ కూడా తయారు చేయవచ్చు.
భాగ పరీక్షతో ప్రారంభించండి. అది p/q రూపంలో ఉండగలదా, ఇక్కడ p, q పరిమిత మరియు q ≠ 0? అవును అంటే అది రేషనల్. దశాంశ రూపం ముగుస్తుంది లేదా తిరిగిపోతుంది (0.125 లేదా 0.333… వంటి) అయితే అది రేషనల్. అది ముగియకుండా తిరగకపోతే (π లేదా √2 దశాంశాల వంటి) అది అసంగతం. పరిమిత సంఖల కోసం, n = n/1 కనుక ప్రతి పరిమితం రేషనల్; అందువల్ల 0 రేషనల్ ఎందుకంటే 0 = 0/1. ఈ తనిఖీలు సమానంగా వర్తిస్తాయి.
- 🧩దశ 1: integer p/q ప్రయత్నించండి; q = 0 వెంటనే తిరస్కరించండి.
- 🔎 దశ 2: దశాంశాలను పరిశీలించండి: ముగిసిన లేదా తిరిగే → రేషనల్.
- 🧱 దశ 3: integerలు ఆటో అర్హత పొందతారు (n = n/1), ఇందులో 0 కూడా.
- 🛑 దశ 4: రెండు దశలూ తప్పయితే మరియు దశాంశం తిరిగిపోకపోతే → అసంగతం.
- 🗂️ దశ 5: సెట్ సభ్యత్వాన్ని గుర్తుంచుకోండి (పూర్తి, పరిమిత, వాస్తవ) పూర్తి మార్కుల కోసం.
| మూల్యం 🔢 | భాగ రూపం | రేషనల్? ✅/❌ | సెట్ ట్యాగ్లు 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | పరిమిత, పూర్తి, వాస్తవ |
| −3/4 | −3/4 | ✅ | రేషనల్, వాస్తవ |
| 0.125 | 1/8 | ✅ | రేషనల్, వాస్తవ |
| 0.333… | 1/3 | ✅ | రేషనల్, వాస్తవ |
| √2 | — | ❌ | అసంగతం, వాస్తవ |
| π | — | ❌ | అసంగతం, వాస్తవ |
మల్టీమీడియా బలపరిచే అవసరం ఉందా? ఒక చిన్న వివరణ వీడియో రేషనల్ మరియు అసంగత మధ్య గడువు లను స్థిరపరుస్తుంది, శూన్యాన్ని కేంద్రముగా ఉంచుతూ. ఉపాధ్యాయులు ప్లేలిస్ట్ తయారుచేయాలంటే, నిర్మిత ప్రశ్నలతో కాంప్రెస్డ్ క్లిప్లను surface చేయవచ్చు.
సాంకేతికంగా ఆలోచించే విద్యార్థులు చాలా సార్లు నోట్ వ్యవస్థలు, పైప్లైన్లు ఏర్పాట్లు చేస్తారు; మీ శైలి అయితే, వర్చువలైజ్డ్ మీడియా సర్వర్లు అధ్యయన వనరులు ఆహ్వానిస్తాయి, మరియు API సాధనాల ద్వారా టాస్క్ ఆటోమేషన్ 0, 0/0 (నిర్వచన రహితం), 1/0(నిర్వచన రహితం) వంటి సరిహద్దు కేసులపై దృష్టి పెట్టిన ప్రాక్టీస్ డెక్కులు రూపొందించగలవు. శుభ్రమైన పైప్లైన్ స్పష్టమైన నిర్వచనాన్ని బలోపేతం చేస్తుంది.
ఈ విభాగానికి తుది ఆలోచన: సజావుగా ఉండటం విజయం. శూన్యం ప్రతినిధులుగా సమాన రీతిగా ప్రవర్తించి, సార్టర్కి పర్ఫెక్ట్ ఆంకర్గా నిలుస్తుంది.
గడువు మార్గాల్లో ప్రయోగాలు: స్థాన విలువు, డేటా వ్యవస్థలు, మరియు తరగతి కథనాలలో శూన్యం ముఖ్యమైన చోటు
శూన్యం రేషనలిటీ కేవలం ఒక నిరూపణ కాదు; అది సమాచారం వ్యవస్థలు మరియు విద్యా పద్ధతులు ఎలా ప్రవర్తిస్తాయో ఆధారపెడుతుంది. పదార్థ-పదవిలో, ‘0’ అంకె ఆ స్థానంలో “ఏమీ లేదు” అని సూచిస్తుంది, ఇది పరిమాణాన్ని సరైనట్లు ఉంచుతుంది: 101 11 నుండి భిన్నం ఎందుకంటే మధ్య ‘0’ స్థానాన్ని ఖాళీగా ఉంచుతుంది. స్ప్రెడ్షీట్లలో మరియు కోడులో, శూన్యం తరచుగా “ఏ అంశాలు లేవు”, “ఏ తప్పులు లేవు”, లేదా ప్రాథమిక స్థితి అని సూచిస్తుంది—ఇది లెక్కింపులకు నిర్దిష్టత ఇస్తుంది. కలపకపోవడం వల్ల 0 లోని వైఫల్యం డాష్బోర్డులు, సమయ గణితం, మరియు ఆల్గోరిథమ్లకు గందరగోళాన్ని తెస్తుంది.
డేటా వర్గీకరణ పనులను పరిగణించి: ఒక కాలమ్ లో కేవలం రేషనల్ సంఖ్యలు నిల్వ చేయాలనుకుంటే, శూన్యం తప్పనిసరి, లేదా ప్రాథమిక స్థితిలో ఉన్న మాపులను తిరస్కరించాల్సి వస్తుంది. మాయా ఒక చిన్న “డేటా హైజీన్” ప్రదర్శన రూపొందిస్తుంది: ఒక పార్సర్కు పరిమిత, సులభ భాగాలు, తిరిగే దశాంశాలు మరియు తెలిసిన అసంగతాలను మిశ్రమంగా ఇస్తుంది; ధృవీకర్త q ≠ 0 కలిగిన p/q లోకి మార్చగల దేమున్నది ఎవరైనా అంగీకరిస్తుంది. ప్రదర్శనలో 0 ని పరిమిత మరియు భాగపు మార్గాలలో చెలామణి చేస్తుంది. ఈ స్థలంలో విద్యార్థులు యూనిట్ టెస్టులు వ్రాసి 0 తో గుణించడం మరియు జోడించడం మూసి సంరక్షణ జరగడం నిర్ధారిస్తారు.
- 🧮 స్థాన విలువు: 0 అంకెలు సవరించకుండా ఉంచి, పరిమాణ తప్పులు నివారిస్తాయి.
- 🧰 డేటా స్థిరత్వం: రేషనల్ మాత్రమేని ఫీల్డుల్లో 0 తప్పక ఒప్పుకుంటుంది.
- 🧷 లోపాల నిర్వహణ: 1/0 లోపాలు పార్స్ సమయంలో గుర్తిస్తారు, runtime కాదు.
- 🧪 పరీక్షలు: రేషనల్స్ లో మూసి లక్షణాల టెస్టులో 0 ని చేర్చండి.
- 📚 కథనం: మాయా 0 ని “ఆంకర్” గా పాఠ్య సజీవపత్రాలు మరియు ప్రాజెక్ట్ డాక్స్ లో లేబుల్ చేస్తుంది.
| પરિસ્થિતિ 🗂️ | 0 యొక్క పాత్ర | రేషనలిటీ ఎలా సహకరిస్తుంది 🎓 | తరగతి సంకేతం 🛎️ |
|---|---|---|---|
| స్థాన విలువ | ఖాళీ స్థానాలను కలిగి ఉంటుంది | అనుకూల మోతాదును అర్థం చేసుకోవడం | “0 సీటుని వేడి చేస్తుంది” 😊 |
| ధృవీకరణ | 0/1గా అంగీకరించబడింది | విలువైన ఇన్పుట్ పరిమిత పరిమితులు | 0, 1/0, 0/0 వేరుగా పరీక్షించండి |
| హిసాబు చేయడం | యోడించే గుర్తింపు | సూక్ష్మీకరణ నిర్దిష్టతలు మరియు కోడ్ సులభం | యూనిట్ టెస్టుల్లో 0 ని ఉపయోగించండి |
| బోధన | ఆంకర్ ఉదాహరణ | భ్రమలు తగ్గిస్తుంది | ఉదాహరణలు 0 తో ప్రారంభించండి |
ఆసక్తి విరామం: గణితం గురించి సంభాషణకు స్పష్టమైన భాష మరియు సందర్భం అవసరం. గణితం బయట కూడా, స్పష్టత ముఖ్యం — whether it’s parsing emoji అర్ధాలు పాఠశాల ఫోరమ్లలో ტోన్ కోసం, పాఠశాల సురక్షిత సాంకేతికతని మూల్యాంకనం చేయడం, లేదా వార్తా కథనాలను గుర్తించడం లోనూ. పాఠం ఇది: నిర్వచనలు, పరిమితులు, మరియు ఉదాహరణలు గందరగోళాన్ని నివారిస్తాయి. అదే సమయం, ఒక సాధారణ తాము తవ్వటం లాంటి ప్రతీక పాఠం కూడా learners కు తార్కికంగా ఎలా అర్థాలు వాకినట్లు మారుతాయో గుర్తు చేస్తుంది — రేషనల్ నిర్వచనం కాబట్టి శూన్యం స్థిరంగా ఉంటుంది.
ఈ విభాగానికి ముగింపు తత్త్వం: శూన్యం రేషనలిటీ కేవలం లేబుల్ కాదు; ఇది సంఖ్యా గణితం నుండి విశ్లేషణ వరకు వ్యవస్థలు ఎప్పటికప్పుడు ఊహించదగినదిగా ఉంచే హామీ.
మాయా యొక్క మినీ-సెట్ తో అదనపు సాధన
మాయా విద్యార్థులు ఈ సంఖ్యలను ఒక నిమిషంనుండి తక్కువ సమయంలో వర్గీకరిస్తారు: 0, −7, 2/9, 0/3, 3/0, 0.1010010001…, మరియు √9. ఫలితాలు: 0 (రేషనల్), −7 (రేషనల్), 2/9 (రేషనల్), 0/3 (రేషనల్), 3/0 (నిర్వచన రహితం), 0.1010010001… (తిరగని, ముగియనిది → చాలా సాద్యంగా అసంగతం), √9 (3 కు సమానం → రేషనల్). నమూనాలను గ్రహించే నైపుణ్యం యూనిట్లు మరియు పరీక్షల మీద గుండా బదిలీ అవుతుంది.
{“@context”:”https://schema.org”,”@type”:”FAQPage”,”mainEntity”:[{“@type”:”Question”,”name”:”Is zero considered a rational number?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Yes. By definition, a rational number is any value expressible as p/q with integers p and q and q u2260 0. Zero fits because 0 = 0/1, 0/5, or 0/n for any nonzero integer n.”}},{“@type”:”Question”,”name”:”Does division by zero make zero non-rational?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”No. Division by zero is a rule about denominators, not about the number zero. 5/0 and 0/0 are undefined expressions, but 0 itself remains a valid rational number.”}},{“@type”:”Question”,”name”:”Is zero an integer, whole, or natural number?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Zero is an integer and a whole number. Whether it is a natural number depends on convention: many courses start naturals at 1, while some contexts include 0.”}},{“@type”:”Question”,”name”:”Can zero be written as a decimal and still be rational?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Yes. Zerou2019s decimal form is 0.0 (or 0.000u2026), which is terminating. Terminating and repeating decimals are rational by definition.”}},{“@type”:”Question”,”name”:”How does zerou2019s role help in algebra?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Zero is the additive identity: a + 0 = a. It keeps equations balanced and simplifies proofs. Multiplying any rational number by 0 gives 0, which is rational.”}}]}శూన్యం రేషనల్ సంఖ్యగా పరిగణించబడుతుందా?
అవును. నిర్వచనం ప్రకారం, రేషనల్ సంఖ్య అంటే integer p మరియు q గల p/q రూపంలో వ్రాయగల ఏ విలువ. ఈ q ≠ 0 అయి ఉండాలి. 0 సరిపోతుంది ఎందుకంటే 0 = 0/1, 0/5 లేదా 0/n ఏ సున్నా కాని integer n కోసం.
సున్నాతో భాగాకరణ శూన్యాన్ని రేషనల్ కాకుపరుస్తుందా?
లేదు. సున్నాతో భాగాకరణ నియమం హ్రాసకం గురించి, శూన్యం మీద కాదు. 5/0 మరియు 0/0 నిర్వచన రహితమైన వ్యక్తీకరణలు, కానీ 0 తాను సరైన రేషనల్ సంఖ్యగా ఉంటుంది.
శూన్యం integer, పూర్తి లేదా స్వభావిక సంఖ్యా?
శూన్యం integer మరియు పూర్తి సంఖ్య. అది స్వభావిక సంఖ్య కాదా అన్నది సంప్రదాయం మీద ఆధారపడుతుంది: చాలా కోర్సులు స్వభావిక సంఖ్యలు 1 నుండి ప్రారంభిస్తాయి, కొన్నిసార్లు 0 ను చేర్చుతాయి.
శూన్యాన్ని దశాంశంగా వ్రాసిన రెండూ రేషనల్ గా ఉంటుందా?
అవును. శూన్యం దశాంశం 0.0 (లేదా 0.000…)గా ఉంటుంది, ఇది ముగిసిన దశాంశ. ముగిసే మరియు తిరుగే దశాంశాలు నిర్వచన ప్రకారం రేషనల్.
శూన్యం బీజగణితంలో పాత్ర ఎలా సహకరించును?
శూన్యం యోడించే గుర్తింపు: a + 0 = a. ఇది సమీకరణాలను సమతుల్యం చేస్తుంది మరియు నిరూపణలను సులభం చేస్తుంది. ఏ రేషనల్ సంఖ్యను 0 తో గుణిస్తే 0 వస్తుంది, ఇది రేషనల్.

-

 సాంకేతికత1 day ago
సాంకేతికత1 day agoమీ కార్డు ఈ రకం కొనుగోలును మద్దతు ఇవ్వదు: దీని అర్థం ఏమిటి మరియు దీనిని ఎలా పరిష్కరించాలి
-

 ఏఐ మోడల్స్1 day ago
ఏఐ మోడల్స్1 day agoOpenAI vs Tsinghua: 2025 లో మీ AI అవసరాలకు ChatGPT మరియు ChatGLM మధ్య ఎంపిక
-

 ఇంటర్నెట్23 hours ago
ఇంటర్నెట్23 hours agoభవిష్యత్తును అన్వేషించడం: 2025లో ఇంటర్నెట్-సమర్ధ ChatGPT గురించి మీకు తెలుసుకోవలసినది
-

 ఏఐ మోడల్స్13 hours ago
ఏఐ మోడల్స్13 hours agoచాట్జిపిటి పరిణామం: 2025లో ఆర్టిఫిషియల్ ఇంటెలిజెన్స్ మన దైనందిన పరస్పర చర్యలను ఎలా విప్లవీకరించింది
-

 ఏఐ మోడల్స్1 day ago
ఏఐ మోడల్స్1 day ago2025లో మీ AI పరిశోధనా సహచరుడిని ఎంచుకోవడం: OpenAI vs. Phind
-

 సాంకేతికత10 hours ago
సాంకేతికత10 hours agoమోసపూరిత కఠినతను అర్థం చేసుకోవడం: దీని అర్ధం మరియు 2025లో ఇది ఎందుకు ముఖ్యం