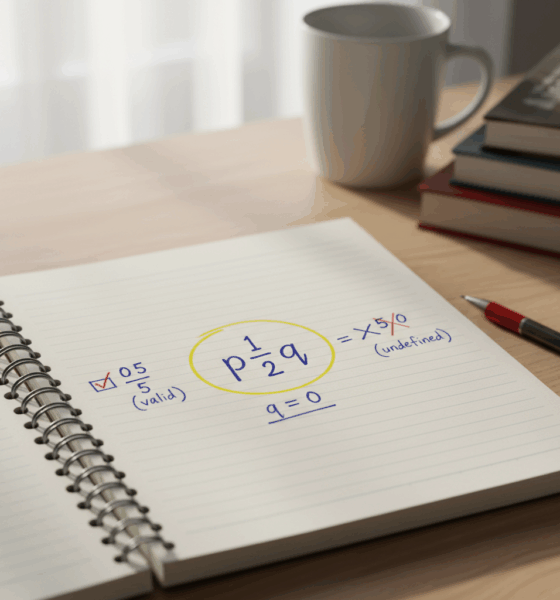
Tech
le zéro est-il considéré comme un nombre rationnel ? expliqué simplement
Le zéro est-il considéré comme un nombre rationnel ? Une explication simple qui tient
Demandez à n’importe quel élève qui lutte avec les fractions : le zéro est-il un nombre rationnel ? La réponse claire en mathématiques est oui. Un nombre rationnel est toute valeur pouvant s’écrire comme une fraction p/q où p et q sont des entiers, et où le dénominateur q n’est pas nul. Puisque 0 peut s’exprimer comme 0/1, 0/7 ou plus généralement 0/n pour tout entier n non nul, cela s’intègre parfaitement. Mais l’histoire devient plus riche quand on élargit le regard à la théorie des nombres, aux limites, et à la manière dont les apprenants intègrent les concepts mathématiques. Pour garder les choses accessibles, voici Maya, une codeuse lycée qui fait du tutorat pour des plus jeunes ; elle apprécie une explication simple appuyée par des exemples clairs et la détection de motifs.
Maya commence par une checklist rapide. Si un nombre a une forme fractionnaire valide avec un numérateur entier et un dénominateur non nul, il est rationnel. Le zéro passe le test car son numérateur peut être 0 tandis que son dénominateur peut être n’importe quel entier non nul. La division par zéro est interdite, mais cette règle concerne le dénominateur, pas le nombre zéro lui-même. En classe, cette distinction évite le classique malentendu : 0/5 est valide (et égale 0), tandis que 5/0 est indéfini. Cette simple ligne sauve des heures de confusion.
Pour les apprenants qui aiment le contexte, le zéro appartient aussi à d’autres ensembles. C’est un entier (…−2, −1, 0, 1, 2…), un nombre entier naturel (0, 1, 2, 3, …), et un nombre réel (faisant partie du continuum complet incluant rationnels et irrationnels). Cependant, de nombreux manuels définissent les nombres naturels comme commençant à 1, excluant ainsi 0 ; certains contextes en informatique incluent 0 comme naturel. Connaître la convention utilisée dans un cours évite des débats inutiles.
Dans les classes de 2025, les enseignants utilisent de plus en plus l’IA et les explications pour rendre ces distinctions mémorables. Les outils qui aident à organiser les exemples—comme les tableaux de projets et les planificateurs de contenu—reflètent la rigueur des définitions des fractions. Pour un aperçu de la manière dont les outils de pensée structurée transforment les flux d’apprentissage, des ressources sur l’automatisation avec les API ou un aperçu des tendances technologiques axées sur l’éducation illustrent comment la clarté se déploie à grande échelle. Même des explorations insolites—comme ce que représente un milliard de secondes—peuvent contextualiser les nombres grands et petits que l’on retrouve dans les leçons sur les fractions et la valeur de position.
- ✅ Le zéro est rationnel parce qu’il équivaut à 0/n avec n ≠ 0.
- 🚫 La division par zéro (comme 5/0) est indéfinie, sans lien avec la rationalité de zéro.
- 🧩 Le zéro appartient à plusieurs ensembles : entiers, nombres entiers naturels, et réels.
- 🧠 Les conventions varient pour les naturels ; vérifiez la définition dans votre cours.
- 🎯 Utilisez le test de fraction : numérateur entier et dénominateur non nul.
| Nombre 🔢 | Rationnel ? ✅/❌ | Raison 💡 |
|---|---|---|
| 0 | ✅ | Peut s’écrire comme 0/1, 0/5, … avec numérateur entier et dénominateur non nul. |
| 5 | ✅ | Égale 5/1 (forme fractionnaire entière). |
| 1/3 | ✅ | Numérateur et dénominateur entiers ; la décimale est périodique. |
| π | ❌ | Ne peut pas s’exprimer comme un rapport d’entiers ; décimale non périodique. |
| √2 | ❌ | Irrationnel prouvé ; aucune fraction entière égale √2. |
Idée clé à retenir : la définition fractionnaire seule règle le statut du zéro—sans drame, juste de la structure.

Passer de la forme fractionnaire aux usages réels du zéro
Avant d’aborder les propriétés, Maya pose une question pratique : où le zéro apparaît-il en dehors des feuilles d’exercices ? Dans les budgets, une ligne zéro signifie aucune dépense ; en code, 0 signale faux ou vide ; dans les tableaux de bord, 0 marque la ligne de base. La même clarté nécessaire pour traiter 0 comme rationnel aide les équipes à étiqueter, comparer et calculer sans ambiguïté. Pour les développeurs qui expérimentent avec des utilitaires temporels, comprendre zéro comme un décalage de départ s’aligne avec des outils fiables comme la récupération précise du temps en Swift pour l’arithmétique des intervalles.
Pourquoi 0 correspond à la définition du nombre rationnel : fractions, décimales et algèbre
Au-delà de la définition formelle, la polyvalence du zéro en tant que nombre rationnel apparaît dans plusieurs représentations. Dans toute fraction p/q, si p = 0 et q ≠ 0, la valeur est 0. C’est pourquoi 0/1 = 0/9 = 0/−13 = 0. Changer le signe ou modifier le dénominateur ne change pas la valeur car multiplier ou diviser zéro par un entier non nul donne toujours zéro. Cela fait de 0 la valeur fractionnaire la plus stable sous les transformations équivalentes.
Les décimales racontent la même histoire. Un nombre rationnel a une expansion décimale finie ou périodique. La décimale de zéro est 0,0, 0,000…, ou toute chaîne équivalente avec un nombre fini ou infini de zéros à la suite—toutes ces options sont finies en pratique. Si un élève voit 0,000, l’essentiel est qu’il n’y a pas de chiffres non nuls après la virgule ; donc c’est rationnel et équivaut à 0.
L’algèbre approfondit l’intuition. Le zéro est l’élément neutre additif : pour tout nombre a, a + 0 = a. Cette identité s’accorde bien avec les règles de l’arithmétique rationnelle. Par exemple, ajouter 0 à un nombre rationnel p/q maintient p/q rationnel. Multiplier un rationnel par 0 donne 0, qui est encore rationnel. Les propriétés de fermeture des rationnels et le rôle spécial du 0 se renforcent mutuellement : rien ne casse quand zéro entre en jeu.
Maya montre une routine en classe que les élèves peuvent recopier dans leurs notes ou flashcards. La routine évite les raccourcis et fait ressortir les règles qui comptent vraiment.
- 🧪 Test de fraction : écrire le nombre sous la forme p/q avec p, q entiers et q ≠ 0 → rationnel.
- 🔁 Test décimal : fini ou périodique → rationnel (la décimale de 0 est constituée uniquement de zéros).
- ➕ Vérification de l’identité : ajouter 0 ne change rien ; multiplier par 0 donne 0.
- 🧭 Vérification des signes : 0/−7 = 0/7 = 0 ; le signe dans le dénominateur n’a pas d’importance.
- ⚠️ Alerte : un dénominateur égal à 0 rend l’expression indéfinie, pas « irrationnelle ».
| Représentation 🧮 | Exemple | Rationnel ? 🔍 | Raisonnement 🧠 |
|---|---|---|---|
| Fraction | 0/19 | ✅ | Numérateur entier et dénominateur non nul → valeur 0. |
| Décimale | 0,000… | ✅ | Forme décimale finie (ou pratiquement finie). |
| Forme entière | 0 | ✅ | Tout entier est rationnel (n = n/1). |
| Nombre mixte | 0 0/5 | ✅ | Equivalent à 0 ; la partie fractionnaire disparaît. |
| Notation scientifique | 0,0 × 10³ | ✅ | Toujours 0 ; la notation n’affecte pas la rationalité. |
Pour les apprenants qui apprécient les croisements avec la technologie, les coachs de rédaction assistés par IA peuvent aider les explications à rester cohérentes ; voyez comment un coach d’écriture pour la clarté ou des bibliothèques sélectionnées pour des sorties structurées reflètent la fiabilité des règles de fraction. Et si le suivi du progrès s’étale sur plusieurs semaines, des utilitaires comme les compteurs basés sur le calendrier sont des compagnons pratiques.
En résumé : qu’il soit écrit en fraction, en décimale ou en entier, le zéro reste rationnel — et cette constance est ce qui le rend si utile.
Idées reçues courantes sur le zéro : division, limites et cas « compliqués »
La plus grande confusion autour du zéro vient du mélange de règles distinctes. Le piège classique est de confondre « division par zéro indéfinie » avec « zéro qui ne serait pas rationnel ». Ces deux notions n’ont rien à voir. Dans une fraction p/q, la seule interdiction est q = 0. Poser p = 0 est autorisé et sans risque. Maya utilise une comparaison rapide : un dénominateur zéro, c’est comme demander des places dans un vol qui n’existe pas — aucun billet ne corrigera cela. Mais avoir un numérateur zéro signifie juste qu’aucun passager ne s’est présenté ; le vol existe toujours.
Les limites créent ensuite un nœud. Considérons lim (x→0) 1/x. Approché par la droite, on tend vers +∞ ; par la gauche, on plonge vers −∞. Cela nous informe sur le comportement près de zéro, pas sur la valeur du zéro ni sur sa rationalité. De même, les « formes indéterminées » comme 0/0 apparaissent en calcul différentiel lors de l’évaluation des limites, mais l’expression 0/0 est indéfinie en tant que nombre. Aucune de ces idées analytiques ne remet en question l’appartenance du zéro à l’ensemble rationnel.
D’autres points délicats surgissent en combinatoire et en algèbre. La factorielle 0! vaut 1 par définition (conforme à la récursion et à la logique du produit vide), ce qui est rationnel. L’exponentiation peut aussi sembler curieuse : 0^0 est souvent laissée indéfinie car des extensions concurrentes viendraient contredire des propriétés souhaitables ; en mathématiques discrètes, on la prend parfois comme 1 pour simplifier les formules. Quoi qu’il en soit, la valeur 0 reste rationnelle.
- 🧯 Mythe : « La division par zéro prouve que 0 n’est pas rationnel. » Réalité : seuls les dénominateurs ne peuvent pas être 0 ; les numérateurs le peuvent.
- 📉 Mythe : « Les limites en 0 définissent ce qu’est zéro. » Réalité : les limites décrivent le comportement proche, pas l’identité du zéro.
- 🧩 Fait : 0! = 1 → rationnel ; 0^0 dépend du contexte mais n’affecte pas la rationalité du zéro.
- 🔄 Fait : les décimales périodiques indiquent la rationalité ; la décimale de zéro est une répétition triviale de 0.
- 🧭 Astuce : gardez les règles arithmétiques, les lois des limites et les définitions d’ensembles dans des tiroirs mentaux séparés.
| Expression/Idée 🧠 | Statut | Impact sur la rationalité de zéro 🎯 | Conseil pour l’élève ✍️ |
|---|---|---|---|
| 5/0 | Indéfini ❌ | Aucun ; sans rapport avec le fait que 0 soit rationnel. | Le dénominateur ne peut pas être 0. Point final. |
| 0/5 | Valide ✅ | Confirme que 0 est un nombre rationnel. | Tout dénominateur non nul convient. |
| lim (x→0) 1/x | Pas de limite finie | Ne classe pas 0 ; décrit le comportement proche de 0. | Séparez le calcul différentiel de l’arithmétique. |
| 0! | Égale 1 | Rationnel (1/1) ✅ | Convention du produit vide. |
| 0^0 | Contexte-dépendant | Pas de changement du statut du zéro | Suivez les règles de votre cours. |
Quand les modèles mentaux ont besoin d’affinage, des flux de travail bien structurés aident. Des articles sur l’amélioration de la discipline d’évaluation, comme mesurer ce qui compte dans les classes de 2025, ou la gestion des changements de contexte, comme dans la gestion des fenêtres de contexte, montrent comment des définitions précises évitent les erreurs de catégorie. Des catégories claires sont précisément ce qui maintient le zéro rationnel et la division par zéro hors limites—deux vérités qui cohabitent harmonieusement.

Passerelle vers l’histoire et les axiomes
Les élèves demandent souvent : si les règles sont si claires, pourquoi l’humanité a-t-elle eu du mal à adopter le zéro ? C’est le préambule parfait à l’histoire des zéros en tant que marqueurs de position, des marchands, et des axiomes qui ont cimenté les définitions actuelles.
Des marqueurs anciens aux axiomes modernes : comment le zéro a gagné sa place
Le chemin du zéro de « rien » à un nombre à part entière fut loin d’être immédiat. Les scribes babyloniens utilisaient un symbole de placeholder pour garder la valeur de position claire, mais le concept de zéro comme nombre autonome a pris racine en Inde, avec des mathématiciens comme Brahmagupta articulant l’arithmétique avec zéro vers le 7e siècle. Le commerce et la recherche ont diffusé ces idées à travers le monde islamique puis en Europe, où la résistance s’est peu à peu estompée à mesure que la notation positionnelle s’est imposée comme indispensable en commerce et astronomie. L’essor de l’algèbre, puis du calcul, ont fixé la centralité du zéro.
Les approches axiomatiques modernes rendent la classification étanche. À partir de structures comme les axiomes de Peano pour les naturels, les mathématiciens construisent les entiers à partir de classes d’équivalence de paires de naturels, et les rationnels à partir de classes d’équivalence de paires d’entiers (p, q) avec q ≠ 0. Dans cette construction, la classe [(0, 1)] représente le nombre rationnel 0—claire et sans ambiguïté. C’est pourquoi les manuels affirment sans hésitation que zéro est rationnel. La seule marge d’interprétation concerne la manière dont on définit les « nombres naturels » incluant ou excluant zéro ; chaque choix est cohérent, mais les enseignants doivent préciser leur convention.
Maya utilise une courte frise chronologique pour aider les apprenants à ancrer l’évolution. Cela donne l’impression que la définition actuelle est le résultat d’un long projet d’ingénierie : les pièces s’emboîtent parce qu’elles ont été conçues pour.
- 📜 Les marqueurs à Babylone antique ont préparé la notation positionnelle.
- 🧮 Les mathématiciens indiens ont formalisé l’arithmétique avec zéro et les nombres négatifs.
- 🌍 Le transfert de connaissances par le commerce a solidifié zéro dans les mathématiques mondiales.
- 🏛️ Les axiomes modernes dérivent les rationnels des entiers avec q ≠ 0.
- 🔧 L’informatique et la science des données ont standardisé le rôle du zéro dans l’indexation et la logique.
| Ère ⏳ | Étape clé | Impact sur la rationalité de 0 🎯 | Mnémonique 📌 |
|---|---|---|---|
| Antiquité | Apparition du placeholder | Prépare la pensée positionnelle mais pas encore un nombre | « Place vide » sur la ligne des chiffres |
| Inde classique | 0 comme nombre avec opérations | Les règles arithmétiques se stabilisent | 0 × a = 0, a + 0 = a |
| Transmission médiévale | Commerce et savoir diffusent la valeur de position | La notation se standardise | Les marchands ont besoin des zéros |
| axiomes modernes | Construction des ℚ à partir des entiers via les paires (p, q) | [(0, 1)] correspond au rationnel 0 ✅ | q ≠ 0 est la seule contrainte |
Les éducateurs d’aujourd’hui mélangent souvent contexte historique et outils numériques pour améliorer la rétention. Les blogs pédagogiques qui dévoilent les enjeux sensibles liés à la tech—comme des débats juridiques impliquant l’IA—montrent l’importance des définitions précises. De même, des articles comparant des assistants, comme Copilot vs ChatGPT, rappellent que des règles cohérentes aboutissent à des résultats fiables. Même les discussions sur la gestion des données ou l’analyse de fichiers renforcent une leçon essentielle : des entrées propres et des contraintes claires—comme q ≠ 0—gardiens de la stabilité des systèmes.
À retenir pour les apprenants : le zéro n’est pas apparu par hasard ; il a été intégré dans le système numérique, et son statut rationnel est garanti par construction.
Raisonnement pratique : classer rapidement les nombres (avec zéro comme référence)
Avec la vue d’ensemble en place, Maya lance un « trieur de 90 secondes » pour les exercices. L’idée est de classifier rapidement toute entrée en vérifiant la forme fractionnaire, le comportement décimal, et l’appartenance aux ensembles—en prenant zéro comme cas pivot. Le but est la rapidité sans négligence. Les apprenants peuvent même construire une mini antisèche pour les marges de contrôles.
Commencez par le test de fraction. Peut-il s’écrire p/q avec p, q entiers et q ≠ 0 ? Si oui, c’est rationnel. Si la forme décimale est finie ou périodique (comme 0,125 ou 0,333…), c’est rationnel. Si elle ne finit pas et ne répète pas (comme π ou √2 en décimale), c’est irrationnel. Pour les entiers, rappelez-vous que n = n/1 rend chaque entier rationnel ; ainsi 0 est rationnel car 0 = 0/1. Ces vérifications s’appliquent uniformément dans les exercices.
- 🧩 Étape 1 : Essayez p/q avec parties entières ; rejetez q = 0 immédiatement.
- 🔎 Étape 2 : Inspectez les décimales : finie ou périodique → rationnel.
- 🧱 Étape 3 : Les entiers se qualifient automatiquement (n = n/1), y compris 0.
- 🛑 Étape 4 : Si aucune condition ne tient et que les décimales ne répètent pas → irrationnel.
- 🗂️ Étape 5 : Notez l’appartenance aux ensembles (entier, naturel, réel) pour la pleine note.
| Valeur 🔢 | Forme fractionnaire | Rationnel ? ✅/❌ | Étiquettes d’ensemble 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | Entier, Naturel, Réel |
| −3/4 | −3/4 | ✅ | Rationnel, Réel |
| 0,125 | 1/8 | ✅ | Rationnel, Réel |
| 0,333… | 1/3 | ✅ | Rationnel, Réel |
| √2 | — | ❌ | Irrationnel, Réel |
| π | — | ❌ | Irrationnel, Réel |
Vous voulez un renforcement audiovisuel ? Une vidéo explicative rapide peut ancrer la frontière rationnel vs irrationnel tout en gardant zéro à l’avant-plan. Pour les enseignants qui créent des playlists, des requêtes structurées peuvent aider à trouver des clips concis.
Les apprenants technophiles prototypent souvent des systèmes de notes et des pipelines ; si c’est votre style, des flux modulaires comme les serveurs médias virtualisés peuvent héberger les ressources d’étude, et l’automatisation des tâches via des outils API peut générer automatiquement des cartes d’exercice focalisées sur des cas limites délicats comme 0, 0/0 (indéfini), et 1/0 (indéfini). Un pipeline propre renforce une définition claire.
Dernière réflexion pour cette section : la cohérence l’emporte. Le zéro se comporte de la même façon dans toutes les représentations, ce qui en fait la référence parfaite pour le trieur.
Applications avancées : valeur de position, systèmes de données et scénarios pédagogiques où zéro compte
La rationalité du zéro n’est pas qu’une preuve ; elle sous-tend la cohérence des systèmes d’information et des programmes. En base dix, un chiffre 0 indique « rien à cette position », ce qui conserve la bonne magnitude : 101 diffère de 11 parce que le 0 du milieu maintient la place des dizaines vide. Dans les tableurs et le code, un zéro indique souvent « aucun élément », « pas d’erreur », ou la base—ce qui rend les calculs déterministes. Un traitement désorganisé de 0 injecterait du chaos dans les tableaux de bord, les calculs temporels, et les algorithmes.
Considérez les tâches de classification de données : si une colonne doit stocker uniquement des nombres rationnels, le zéro doit être accepté, sinon des mesures valides à la ligne de base seraient rejetées. Maya conçoit un petit démonstrateur de « hygiène des données » : on fournit à un parseur un mélange d’entiers, fractions simples, décimales périodiques et irrationnels connus ; le validateur accepte tout ce qui se convertit en p/q avec q ≠ 0. La démonstration enregistre 0 comme valide sur les chemins entier et fractionnaire. Ensuite, les étudiants écrivent des tests unitaires pour confirmer la propriété de fermeture sous addition et multiplication avec zéro.
- 🧮 Valeur de position : 0 garde les chiffres alignés, évitant des erreurs de magnitude.
- 🧰 Intégrité des données : zéro doit valider dans les champs rationnels uniquement.
- 🧷 Gestion des erreurs : les erreurs 1/0 sont détectées à l’analyse, pas à l’exécution.
- 🧪 Tests : inclure 0 dans tous les tests de propriétés de fermeture pour les rationnels.
- 📚 Scénario pédagogique : Maya qualifie 0 de « l’ancre » dans les grilles d’évaluation et documents de projet.
| Scénario 🗂️ | Rôle du zéro | Pourquoi la rationalité aide 🎓 | Indication en classe 🛎️ |
|---|---|---|---|
| Valeur de position | Maintient les positions vides | Interprétation de la magnitude cohérente | « 0 garde la place au chaud » 😊 |
| Validation | Accepté comme 0/1 | Contraintes d’entrée claires | Tester 0, 1/0, 0/0 séparément |
| Calcul | Identité additive | Simplifie preuves et code | Utiliser 0 dans les tests unitaires |
| Enseignement | Cas pivot | Réduit la propagation des idées fausses | Commencer les exemples par 0 |
Pause curiosité : la communication autour des mathématiques bénéficie d’un langage précis et d’un contexte clair. Même hors des maths, la clarté compte — que ce soit pour interpréter les significations d’emojis dans les forums étudiants, évaluer la technologie de sécurité scolaire, ou repérer les récits médiatiques. La leçon se transfère : des définitions, contraintes et exemples évitent les confusions. Par le même biais, un piège sans conséquence comme l’interprétation de symboles rappelle comment le sens peut rapidement dévier sans règles partagées—c’est exactement pourquoi la définition rationnelle maintient le zéro ancré.
Clôture de ce segment : la rationalité du zéro dépasse une simple étiquette ; c’est la garantie que les systèmes—from l’arithmétique à l’analytique—restent prévisibles.
Exercices supplémentaires avec le mini-ensemble de Maya
Les élèves de Maya classent ces nombres en moins d’une minute : 0, −7, 2/9, 0/3, 3/0, 0,1010010001…, et √9. Les résultats : 0 (rationnel), −7 (rationnel), 2/9 (rationnel), 0/3 (rationnel), 3/0 (indéfini), 0,1010010001… (non périodique, non fini → vraisemblablement irrationnel), √9 (égal à 3 → rationnel). La capacité à repérer les motifs se transpose dans les unités et contrôles.
{« @context »: »https://schema.org », »@type »: »FAQPage », »mainEntity »:[{« @type »: »Question », »name »: »Le zéro est-il considéré comme un nombre rationnel ? », »acceptedAnswer »:{« @type »: »Answer », »text »: »Oui. Par définition, un nombre rationnel est toute valeur exprimable sous la forme p/q avec p et q entiers et q ≠ 0. Le zéro convient car 0 = 0/1, 0/5, ou 0/n pour tout entier n non nul. »}},{« @type »: »Question », »name »: »La division par zéro rend-elle le zéro non rationnel ? », »acceptedAnswer »:{« @type »: »Answer », »text »: »Non. La division par zéro est une règle concernant les dénominateurs, pas le nombre zéro. 5/0 et 0/0 sont des expressions indéfinies, mais 0 lui-même reste un nombre rationnel valide. »}},{« @type »: »Question », »name »: »Le zéro est-il un entier, un nombre entier naturel ou un nombre naturel ? », »acceptedAnswer »:{« @type »: »Answer », »text »: »Le zéro est un entier et un nombre naturel entier. Qu’il soit un nombre naturel dépend de la convention : de nombreux cours commencent les naturels à 1, tandis que certains contextes incluent 0. »}},{« @type »: »Question », »name »: »Le zéro peut-il être écrit en décimal tout en restant rationnel ? », »acceptedAnswer »:{« @type »: »Answer », »text »: »Oui. La forme décimale du zéro est 0,0 (ou 0,000…), laquelle est finie. Les décimales finies et périodiques sont rationnelles par définition. »}},{« @type »: »Question », »name »: »Comment le rôle du zéro aide-t-il en algèbre ? », »acceptedAnswer »:{« @type »: »Answer », »text »: »Le zéro est l’identité additive : a + 0 = a. Il maintient l’équilibre des équations et simplifie les démonstrations. Multiplier un nombre rationnel par 0 donne 0, qui est rationnel. »}}]}Le zéro est-il considéré comme un nombre rationnel ?
Oui. Par définition, un nombre rationnel est toute valeur exprimable sous la forme p/q avec p et q entiers et q ≠ 0. Le zéro convient car 0 = 0/1, 0/5, ou 0/n pour tout entier n non nul.
La division par zéro rend-elle le zéro non rationnel ?
Non. La division par zéro est une règle concernant les dénominateurs, pas le nombre zéro. 5/0 et 0/0 sont des expressions indéfinies, mais 0 lui-même reste un nombre rationnel valide.
Le zéro est-il un entier, un nombre entier naturel ou un nombre naturel ?
Le zéro est un entier et un nombre naturel entier. Qu’il soit un nombre naturel dépend de la convention : de nombreux cours commencent les naturels à 1, tandis que certains contextes incluent 0.
Le zéro peut-il être écrit en décimal tout en restant rationnel ?
Oui. La forme décimale du zéro est 0,0 (ou 0,000…), laquelle est finie. Les décimales finies et périodiques sont rationnelles par définition.
Comment le rôle du zéro aide-t-il en algèbre ?
Le zéro est l’identité additive : a + 0 = a. Il maintient l’équilibre des équations et simplifie les démonstrations. Multiplier un nombre rationnel par 0 donne 0, qui est rationnel.

-

 Tech1 jour ago
Tech1 jour agoVotre carte ne prend pas en charge ce type d’achat : ce que cela signifie et comment le résoudre
-

 Modèles d’IA1 jour ago
Modèles d’IA1 jour agoOpenAI vs Tsinghua : Choisir entre ChatGPT et ChatGLM pour vos besoins en IA en 2025
-

 Internet23 heures ago
Internet23 heures agoExplorer le futur : Ce que vous devez savoir sur ChatGPT connecté à Internet en 2025
-

 Modèles d’IA1 jour ago
Modèles d’IA1 jour agoChoisir votre compagnon de recherche en IA en 2025 : OpenAI vs. Phind
-

 Tech11 heures ago
Tech11 heures agoComprendre le dur dégénéré : ce que cela signifie et pourquoi cela compte en 2025
-

 Gaming18 heures ago
Gaming18 heures agoGratuit pour tous le combat nyt : stratégies pour maîtriser la bataille ultime