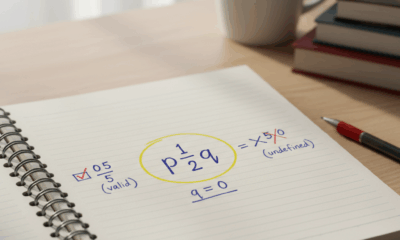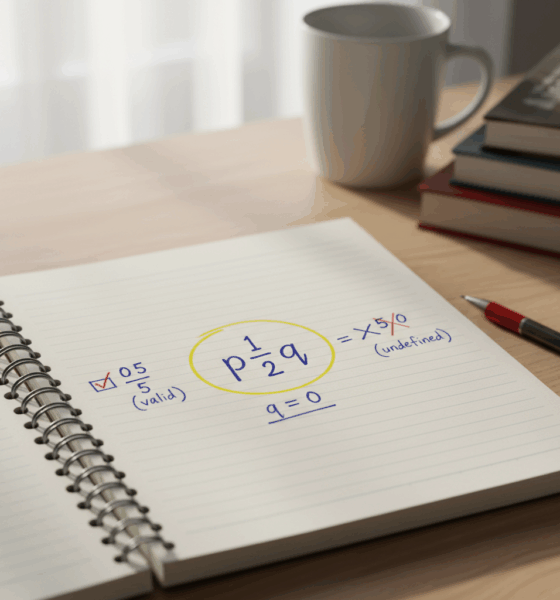
Tecnologia
lo zero è considerato un numero razionale? spiegato semplicemente
Lo zero è considerato un numero razionale? Una semplice spiegazione che resta impressa
Chiedi a qualsiasi studente alle prese con le frazioni: lo zero è un numero razionale? La risposta netta in matematica è sì. Un numero razionale è qualsiasi valore che può essere scritto come una frazione p/q dove p e q sono numeri interi, e il denominatore q non è zero. Dal momento che 0 può essere espresso come 0/1, 0/7 o più generalmente 0/n per qualsiasi intero n diverso da zero, si adatta perfettamente. Ma la questione si arricchisce quando si amplia la prospettiva alla teoria dei numeri, ai limiti e a come gli studenti interiorizzano i concetti matematici. Per mantenere tutto comprensibile, conosciamo Maya, una programmatrice liceale che fa da tutor ai più piccoli; ama una spiegazione semplice supportata da esempi chiari e dal riconoscimento di schemi.
Maya inizia con una lista di controllo veloce. Se un numero ha una forma frazionaria valida con numeratore intero e denominatore diverso da zero, è razionale. Lo zero passa la prova perché il suo numeratore può essere 0 mentre il denominatore può essere qualsiasi intero diverso da zero. La divisione per zero è vietata, ma questa regola riguarda il denominatore, non il numero zero stesso. In classe questa distinzione previene il classico fraintendimento: 0/5 è valido (ed è uguale a 0), mentre 5/0 è indefinito. Questa semplice precisazione salva ore di confusione.
Per chi ama il contesto, lo zero appartiene anche ad altri insiemi. È un intero (…−2, −1, 0, 1, 2…), un numero naturale esteso (0, 1, 2, 3, …) e un numero reale (parte del continuum completo che include valori sia razionali che irrazionali). Tuttavia, molti libri di testo definiscono i numeri naturali come a partire da 1, escludendo lo 0; in alcuni contesti di informatica 0 è incluso come naturale. Sapere quale convenzione usa il corso evita discussioni inutili.
Nelle aule del 2025, gli insegnanti sempre più spesso usano strumenti di intelligenza artificiale e spiegazioni interattive per rendere queste distinzioni memorabili. Strumenti che aiutano a organizzare gli esempi—come lavagne per progetti e pianificatori di contenuti—rispecchiano la chiarezza delle definizioni delle frazioni. Per avere un’idea di come strumenti per il pensiero strutturato stanno trasformando i flussi di apprendimento, risorse su automazione con API o uno sguardo su tendenze tecnologiche in ambito educativo mostrano come la chiarezza si allarghi. Anche esplorazioni più curiose—come cosa si prova con un miliardo di secondi—possono dare contesto a numeri grandi e piccoli presenti nelle lezioni su frazioni e valore posizionale.
- ✅ Lo zero è razionale perché è uguale a 0/n con n ≠ 0.
- 🚫 La divisione per zero (come 5/0) è indefinita, non riguarda la razionalità di zero.
- 🧩 Lo zero appartiene a più insiemi: interi, naturali estesi e reali.
- 🧠 Le convenzioni variano per i numeri naturali; controlla la definizione del tuo corso.
- 🎯 Usa il test della frazione: numeratore intero e denominatore diverso da zero.
| Numero 🔢 | Razionale? ✅/❌ | Motivo 💡 |
|---|---|---|
| 0 | ✅ | Può essere scritto come 0/1, 0/5, … con parti intere e denominatore diverso da zero. |
| 5 | ✅ | Uguale a 5/1 (forma frazionaria intera). |
| 1/3 | ✅ | Numeratore e denominatore interi; decimale è periodico. |
| π | ❌ | Non può essere espresso come rapporto di interi; decimale non periodico. |
| √2 | ❌ | Provato irrazionale; nessuna frazione intera uguale a √2. |
Spunto chiave da ricordare: la definizione di frazione da sola chiarisce lo status dello zero—niente drammi, solo struttura.

Passaggio dalla forma frazionaria agli usi pratici dello zero
Prima di passare alle proprietà, Maya pone una domanda pratica: dove appare lo zero al di fuori dei fogli di esercizi? Nei budget, una riga con zero significa nessuna spesa; nel codice, 0 indica falso o vuoto; nei cruscotti di dati, 0 segna la linea di base. La stessa chiarezza necessaria per considerare 0 razionale aiuta i team a etichettare, confrontare e calcolare senza ambiguità. Per gli sviluppatori che sperimentano con strumenti temporali, comprendere zero come offset iniziale si allinea con strumenti affidabili come il recupero preciso del tempo in Swift per l’aritmetica degli intervalli.
Perché lo 0 rientra nella definizione di numero razionale: frazioni, decimali e algebra
Oltre alla definizione formale, la versatilità dello zero come numero razionale emerge in molteplici rappresentazioni. In qualsiasi frazione p/q, se p = 0 e q ≠ 0, il valore è 0. Ecco perché 0/1 = 0/9 = 0/−13 = 0. Cambiare segno o denominatore non modifica il valore perché moltiplicare o dividere zero per un intero diverso da zero dà sempre zero. Ciò rende 0 il valore frazionario più stabile sotto trasformazioni equivalenti.
I decimali raccontano la stessa storia. Un numero razionale ha uno sviluppo decimale finito o periodico. Il decimale di zero è 0.0, 0.000…, o qualsiasi stringa equivalente con un numero finito o infinito di zeri dopo il punto—ogni opzione è finita di fatto. Se uno studente vede 0.000, la chiave è che non ci sono cifre diverse da zero dopo la virgola; quindi, è razionale e vale 0.
L’algebra approfondisce l’intuizione. Lo zero è l’elemento neutro additivo: per ogni numero a, a + 0 = a. Questa identità si combina bene con le regole dell’aritmetica razionale. Per esempio, aggiungere 0 a un numero razionale p/q mantiene p/q razionale. Moltiplicare qualsiasi razionale per 0 dà 0, che è di nuovo razionale. Le proprietà di chiusura dei numeri razionali e il ruolo speciale dello 0 si rafforzano a vicenda: nulla cambia quando lo zero entra in gioco.
Maya mostra con una routine in classe che gli studenti possono copiare su appunti o flashcard. La routine evita scorciatoie e mette in luce le regole che contano realmente.
- 🧪 Test della frazione: scrivi il numero come p/q con p, q interi e q ≠ 0 → razionale.
- 🔁 Test del decimale: finito o periodico → razionale (il decimale di zero è tutto zero).
- ➕ Controllo identità: aggiungere 0 non cambia; moltiplicare per 0 restituisce 0.
- 🧭 Controllo segno: 0/−7 = 0/7 = 0; il segno nel denominatore non conta.
- ⚠️ Attenzione: denominatore 0 rende l’espressione indefinita, non «irrazionale».
| Rappresentazione 🧮 | Esempio | Razionale? 🔍 | Motivazione 🧠 |
|---|---|---|---|
| Frazione | 0/19 | ✅ | Numeratore intero e denominatore diverso da zero → valore 0. |
| Decimale | 0.000… | ✅ | Forma decimale finita (o effettivamente finita). |
| Forma intera | 0 | ✅ | Ogni intero è razionale (n = n/1). |
| Numero misto | 0 0/5 | ✅ | Equivalente a 0; la parte frazionaria scompare. |
| Notazione scientifica | 0.0 × 10³ | ✅ | Ancora 0; la notazione non influenza la razionalità. |
Per chi apprezza i collegamenti con la tecnologia, i coach di scrittura con intelligenza artificiale possono aiutare le spiegazioni a restare coerenti; guarda come un coach di scrittura per chiarezza o librerie curate come quelle per output strutturati riflettano l’affidabilità delle regole sulle frazioni. E se il progresso va monitorato settimanalmente, utilità come contatori basati su calendario sono ottimi compagni.
In sintesi: che sia scritto come frazione, decimale o intero, lo zero resta razionale—e questa coerenza è ciò che lo rende così utile.
Fraintendimenti comuni sullo zero: divisione, limiti e casi “difficili”
La confusione principale su zero nasce dal mescolare regole diverse. L’errore classico è confondere “la divisione per zero è indefinita” con “lo zero non è razionale”. Non hanno nulla a che fare tra loro. In una frazione p/q, l’unica mossa vietata è q = 0. Impostare p = 0 è consentito e innocuo. Maya usa una metafora veloce: un denominatore zero è come chiedere posti su un volo che non esiste—nessun biglietto lo renderà possibile. Ma avere un numeratore zero significa solo che nessun passeggero si è presentato; il volo esiste comunque.
I limiti creano il nodo successivo. Considera lim (x→0) 1/x. Avvicinandosi da destra si va a +∞; da sinistra a −∞. Ciò ci dice qualcosa sul comportamento vicino a zero, non sul valore di zero o sulla sua razionalità. Allo stesso modo, le “forme indeterminate” come 0/0 compaiono in analisi quando si valutano limiti, ma l’espressione 0/0 è indefinita come numero. Nessuna di queste idee analitiche riduce lo status di zero nel set razionale.
Altri punti complessi emergono in combinatoria e algebra. Il fattoriale 0! vale 1 per definizione (coerente con la ricorsione e la logica del prodotto vuoto), che è razionale. Anche l’esponenziazione può risultare strana: 0^0 è lasciato indefinito in molti contesti perché prolungamenti contrastanti violerebbero proprietà desiderabili; nella matematica discreta, a volte è assunto come 1 per semplificare le formule. Indipendentemente da queste regole ai margini, il valore 0 resta razionale.
- 🧯 Mito: “la divisione per zero dimostra che 0 non è razionale.” Realtà: solo il denominatore non può essere 0; il numeratore può.
- 📉 Mito: “i limiti a 0 definiscono che cos’è zero.” Realtà: i limiti descrivono il comportamento vicino a 0, non l’identità di zero.
- 🧩 Fatto: 0! = 1 → razionale; 0^0 dipende dal contesto ma non cambia la razionalità di zero.
- 🔄 Fatto: i decimali periodici indicano razionalità; il decimale di zero è un triviale ripetersi di 0.
- 🧭 Consiglio: tieni separate le regole aritmetiche, le leggi sui limiti e le definizioni di insieme nella mente.
| Espressione/Idea 🧠 | Stato | Impatto sulla razionalità di zero 🎯 | Consiglio per lo studente ✍️ |
|---|---|---|---|
| 5/0 | Indefinito ❌ | Nessuno; non riguarda se 0 è razionale. | Il denominatore non può essere 0. Punto e basta. |
| 0/5 | Valido ✅ | Conferma 0 come numero razionale. | Qualsiasi denominatore diverso da zero va bene. |
| lim (x→0) 1/x | Nessun limite finito | Non classifica 0; riguarda comportamento vicino a 0. | Separa l’analisi dall’aritmetica. |
| 0! | Uguale a 1 | Razionale (1/1) ✅ | Convenzione del prodotto vuoto. |
| 0^0 | Dipendente dal contesto | Nessuna variazione dello status di zero | Segui le regole del tuo corso. |
Quando i modelli mentali devono essere affinati, flussi di lavoro ben strutturati aiutano. Articoli su come migliorare la disciplina nella valutazione, come misurare ciò che conta nelle classi del 2025, o affrontare cambi di contesto, come con gestire le finestre di contesto, mostrano come definizioni accurate evitino errori di categoria. Le categorie chiare sono esattamente ciò che mantiene zero razionale e la divisione per zero fuori portata—due verità che convivono felicemente.

Ponte tra storia e assiomi
Gli studenti spesso chiedono: se le regole sono così semplici, perché l’umanità ha faticato ad adottare lo zero? È il perfetto collegamento alla storia dei segnaposto, dei mercanti e degli assiomi che hanno cementato le definizioni odierne.
Da segnaposto antico ad assiomi moderni: come lo zero si è guadagnato il suo posto
Il cammino dello zero da “nulla” a numero vero e proprio è stato tutt’altro che immediato. Gli scribi babilonesi usavano un simbolo segnaposto per mantenere il valore posizionale chiaro, ma il concetto di zero come numero autonomo affondò radici in India, con matematici come Brahmagupta che intorno al VII secolo formularono l’aritmetica con zero. Commercio e studi diffusero queste idee attraverso il mondo islamico e l’Europa, dove la resistenza si attenuò gradualmente man mano che la notazione posizionale si dimostrava indispensabile in commercio e astronomia. L’ascesa dell’algebra e poi del calcolo fissarono la centralità dello zero.
Gli approcci assiomatici moderni rendono la classificazione inattaccabile. Partendo da strutture come gli assiomi di Peano per i naturali, i matematici costruiscono gli interi da classi di equivalenza di coppie di naturali, e i razionali da classi di equivalenza di coppie di interi (p, q) con q ≠ 0. In quella costruzione, la classe [(0, 1)] rappresenta il numero razionale 0—pulito e inequivocabile. Ecco perché i testi dichiarano senza esitazione che lo zero è razionale. L’unica incertezza riguarda se i “numeri naturali” includano lo zero; entrambe le scelte sono coerenti, ma gli insegnanti devono dichiarare la loro convenzione.
Maya usa una breve linea temporale per aiutare gli studenti a ancorare l’evoluzione. Fa apparire la definizione attuale come la fine di un lungo progetto di ingegneria: i pezzi combaciano perché sono stati progettati per farlo.
- 📜 I segnaposto nell’antica Babilonia prepararono il terreno per la notazione posizionale.
- 🧮 I matematici indiani formalizzarono l’aritmetica con zero e numeri negativi.
- 🌍 Il trasferimento di conoscenze tramite il commercio consolidò lo 0 nella matematica globale.
- 🏛️ Gli assiomi moderni derivarono i razionali dagli interi con q ≠ 0.
- 🔧 Informatica e data science standardizzarono il ruolo dello zero nell’indicizzazione e nella logica.
| Epoca ⏳ | Traguardo | Impatto sulla razionalità dello 0 🎯 | Gancio mnemonico 📌 |
|---|---|---|---|
| Antica | Emergere del segnaposto | Prepara il pensiero posizionale ma non era ancora un numero | “Posto vuoto” nella linea dei numeri |
| India classica | 0 come numero con operazioni | Le regole aritmetiche si stabilizzano | 0 × a = 0, a + 0 = a |
| Trasmissione medievale | Commercio e studio diffusero il valore posizionale | La notazione si standardizza | I mercanti hanno bisogno dello zero |
| Assiomi moderni | Costruzione di ℚ dagli interi tramite coppie (p, q) | [(0, 1)] è 0 razionale ✅ | q ≠ 0 è l’unico vincolo |
Oggi gli educatori spesso combinano contesto storico con strumenti digitali per migliorare la memorizzazione. Blog di classe che analizzano storie tecnologiche sensibili—come dibattiti legali sull’IA—danno esempio dell’importanza di definizioni precise. Allo stesso modo, articoli di confronto tra assistenti come Copilot vs. ChatGPT riflettono l’idea che regole coerenti portano a risultati affidabili. Perfino discussioni su gestione dati e analisi file rafforzano una lezione: input puliti e vincoli chiari—come q ≠ 0—mantengono i sistemi stabili.
Spunto per gli studenti: lo zero non è comparso dal nulla; è stato ingegnerizzato nel sistema numerico, e il suo status razionale è incorporato nella sua costruzione.
Ragionamento pratico: classificare i numeri rapidamente (con lo zero come ancora)
Con il quadro generale chiaro, Maya propone un “classificatore da 90 secondi” per set di esercizi. L’idea è classificare rapidamente qualsiasi input controllando la forma frazionaria, il comportamento decimale e l’appartenenza agli insiemi—usando lo zero come caso di riferimento. Lo scopo è la velocità senza trascuratezza. Gli studenti possono persino creare una mini tabella riassuntiva per i margini dei test.
Inizia con il test della frazione. Può essere scritto come p/q con p e q interi e q ≠ 0? Se sì, è razionale. Se il decimale finisce o è periodico (come 0,125 o 0,333…), è razionale. Se non finisce né è periodico (come π o √2 come decimali), è irrazionale. Per gli interi, ricorda che n = n/1 fa sì che ogni intero sia razionale; quindi 0 è razionale perché 0 = 0/1. Questi controlli si applicano uniformemente a tutti gli esercizi.
- 🧩 Passo 1: Prova p/q con interi; rifiuta subito q = 0.
- 🔎 Passo 2: Controlla decimali: finito o periodico → razionale.
- 🧱 Passo 3: Gli interi si qualificano automaticamente (n = n/1), incluso 0.
- 🛑 Passo 4: Se nessuna condizione è soddisfatta e i decimali non sono mai periodici → irrazionale.
- 🗂️ Passo 5: Nota l’appartenenza all’insieme (naturali estesi, interi, reali) per il punteggio completo.
| Valore 🔢 | Forma frazionaria | Razionale? ✅/❌ | Tag insiemi 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | Intero, Naturale esteso, Reale |
| −3/4 | −3/4 | ✅ | Razionale, Reale |
| 0,125 | 1/8 | ✅ | Razionale, Reale |
| 0,333… | 1/3 | ✅ | Razionale, Reale |
| √2 | — | ❌ | Irrazionale, Reale |
| π | — | ❌ | Irrazionale, Reale |
Vuoi un rinforzo audiovisivo? Un breve video esplicativo può fissare il confine tra numeri razionali e irrazionali mantenendo lo zero in primo piano. Per gli insegnanti che costruiscono playlist, query strutturate possono aiutare a individuare clip concise.
Gli studenti più tecnologici spesso sperimentano sistemi di appunti e pipeline; se è il tuo stile, flussi modulari come server multimediali virtualizzati possono ospitare risorse di studio, e l’automazione tramite strumenti API può generare automaticamente mazzi di pratica incentrati su casi sfidanti come 0, 0/0 (indefinito) e 1/0 (indefinito). Una pipeline pulita rinforza una definizione chiara.
Pensiero finale per questa sezione: la coerenza vince. Lo zero si comporta sempre allo stesso modo in tutte le rappresentazioni, rendendolo l’ancora perfetta per il classificatore.
Applicazioni di nicchia: valore posizionale, sistemi di dati e contesti scolastici in cui lo zero conta
La razionalità dello zero non è solo una dimostrazione; sostiene il modo in cui i sistemi informativi e i programmi scolastici funzionano. Nel valore posizionale in base dieci, una cifra 0 segnala “nessuna unità in questa posizione”, il che mantiene la magnitudine corretta: 101 è diverso da 11 perché lo 0 centrale conserva la posizione delle decine vuota. Nei fogli di calcolo e nel codice, uno zero indica spesso “nessun elemento”, “nessun errore” o linea di base—rendendo i calcoli deterministici. Un trattamento disorganizzato dello 0 inserirebbe caos in cruscotti, calcoli temporali e algoritmi.
Considera compiti di classificazione dati: se una colonna deve contenere solo numeri razionali, lo zero deve essere ammesso, altrimenti misurazioni legittime alla linea di base verrebbero scartate. Maya progetta una piccola demo “igiene dati”: alimenta un parser con un mix di interi, frazioni semplici, decimali periodici e irrazionali noti; il validatore accetta tutto ciò che è convertibile in p/q con q ≠ 0. La demo registra 0 come valido sia nel percorso intero che frazionario. Da lì, gli studenti scrivono test unitari per confermare la chiusura rispetto a somma e prodotto con zero.
- 🧮 Valore posizionale: lo zero mantiene le cifre allineate, evitando errori di magnitudine.
- 🧰 Integrità dati: lo zero deve essere valido in campi solo razionali.
- 🧷 Gestione errori: errori come 1/0 sono catturati alla fase di parsing, non a runtime.
- 🧪 Test: includi lo zero in tutti i test di proprietà di chiusura per i razionali.
- 📚 Contesto: Maya etichetta 0 come “l’ancora” nelle rubriche e documenti di progetto.
| Scenario 🗂️ | Ruolo dello zero | Perché la razionalità aiuta 🎓 | Segnale in classe 🛎️ |
|---|---|---|---|
| Valore posizionale | Mantiene posizioni vuote | Interpretazione coerente della magnitudine | “Lo zero tiene il posto caldo” 😊 |
| Validazione | Ammesso come 0/1 | Vincoli di input chiari | Testa 0, 1/0, 0/0 separatamente |
| Calcolo | Elemento neutro additivo | Semplifica dimostrazioni e codice | Usa 0 nei test unitari |
| Didattica | Caso di riferimento | Riduce la diffusione di fraintendimenti | Inizia gli esempi con 0 |
Pausa di curiosità: la comunicazione attorno alla matematica beneficia di un linguaggio preciso e del contesto. Anche fuori dalla matematica, la chiarezza conta—sia nel decifrare i significati delle emoji per il tono nei forum studenti, valutare tecnologie per la sicurezza scolastica, o individuare narrative giornalistiche. La lezione si trasferisce: definizioni, vincoli ed esempi evitano fraintendimenti. Allo stesso modo, una piccola deviazione come l’interpretazione di simboli ricorda agli studenti quanto rapidamente il significato possa cambiare senza regole condivise—proprio per questo la definizione di numero razionale mantiene zero saldo.
Insight finale per questo segmento: la razionalità di zero non è solo un’etichetta; è la garanzia che i sistemi—from aritmetica a analisi dati—restino prevedibili.
Ulteriore pratica con il mini-set di Maya
Gli studenti di Maya classificano questi in meno di un minuto: 0, −7, 2/9, 0/3, 3/0, 0.1010010001…, e √9. I risultati: 0 (razionale), −7 (razionale), 2/9 (razionale), 0/3 (razionale), 3/0 (indefinito), 0.1010010001… (non periodico, non finito → probabilmente irrazionale), √9 (uguale a 3 → razionale). L’abilità di riconoscere schemi si trasferisce tra unità e test.
{“@context”:”https://schema.org”,”@type”:”FAQPage”,”mainEntity”:[{“@type”:”Question”,”name”:”Lo zero è considerato un numero razionale?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Sì. Per definizione, un numero razionale è qualsiasi valore esprimibile come p/q con interi p e q e q ≠ 0. Lo zero rientra perché 0 = 0/1, 0/5 o 0/n per ogni intero non nullo n.”}},{“@type”:”Question”,”name”:”La divisione per zero rende lo zero non razionale?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”No. La divisione per zero è una regola sui denominatori, non sul numero zero. 5/0 e 0/0 sono espressioni indefinite, ma lo 0 stesso rimane un numero razionale valido.”}},{“@type”:”Question”,”name”:”Lo zero è un numero intero, naturale esteso o naturale?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Lo zero è un intero e un numero naturale esteso. Se è un numero naturale dipende dalla convenzione: molti corsi considerano naturali i numeri a partire da 1, mentre alcuni contesti includono lo 0.”}},{“@type”:”Question”,”name”:”Lo zero può essere scritto come decimale ed essere comunque razionale?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Sì. La forma decimale di zero è 0.0 (o 0.000…), che è finita. I decimali finiti o periodici sono per definizione razionali.”}},{“@type”:”Question”,”name”:”In che modo il ruolo dello zero aiuta in algebra?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Lo zero è l’elemento neutro additivo: a + 0 = a. Mantiene le equazioni bilanciate e semplifica le dimostrazioni. Moltiplicare un numero razionale per 0 dà 0, che è razionale.”}}]}Lo zero è considerato un numero razionale?
Sì. Per definizione, un numero razionale è qualsiasi valore esprimibile come p/q con interi p e q e q ≠ 0. Lo zero rientra perché 0 = 0/1, 0/5 o 0/n per ogni intero non nullo n.
La divisione per zero rende lo zero non razionale?
No. La divisione per zero è una regola sui denominatori, non sul numero zero. 5/0 e 0/0 sono espressioni indefinite, ma lo 0 stesso rimane un numero razionale valido.
Lo zero è un numero intero, naturale esteso o naturale?
Lo zero è un intero e un numero naturale esteso. Se è un numero naturale dipende dalla convenzione: molti corsi considerano naturali i numeri a partire da 1, mentre alcuni contesti includono lo 0.
Lo zero può essere scritto come decimale ed essere comunque razionale?
Sì. La forma decimale di zero è 0.0 (o 0.000…), che è finita. I decimali finiti o periodici sono per definizione razionali.
In che modo il ruolo dello zero aiuta in algebra?
Lo zero è l’elemento neutro additivo: a + 0 = a. Mantiene le equazioni bilanciate e semplifica le dimostrazioni. Moltiplicare un numero razionale per 0 dà 0, che è razionale.

-

 Tecnologia1 day ago
Tecnologia1 day agoLa tua carta non supporta questo tipo di acquisto: cosa significa e come risolverlo
-

 Modelli di IA1 day ago
Modelli di IA1 day agoOpenAI vs Tsinghua: Scegliere tra ChatGPT e ChatGLM per le tue esigenze di IA nel 2025
-

 Internet23 hours ago
Internet23 hours agoEsplorando il Futuro: Cosa Devi Sapere su Internet-Enabled ChatGPT nel 2025
-

 Modelli di IA1 day ago
Modelli di IA1 day agoScegliere il tuo compagno di ricerca AI nel 2025: OpenAI vs. Phind
-

 Modelli di IA5 hours ago
Modelli di IA5 hours agoScegliere tra Google Bard e ChatGPT di OpenAI: quale soluzione AI è giusta per te nel 2025?
-

 Tecnologia11 hours ago
Tecnologia11 hours agoComprendere hard degenerate: cosa significa e perché è importante nel 2025