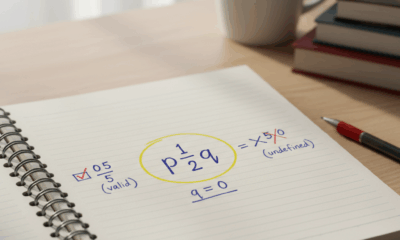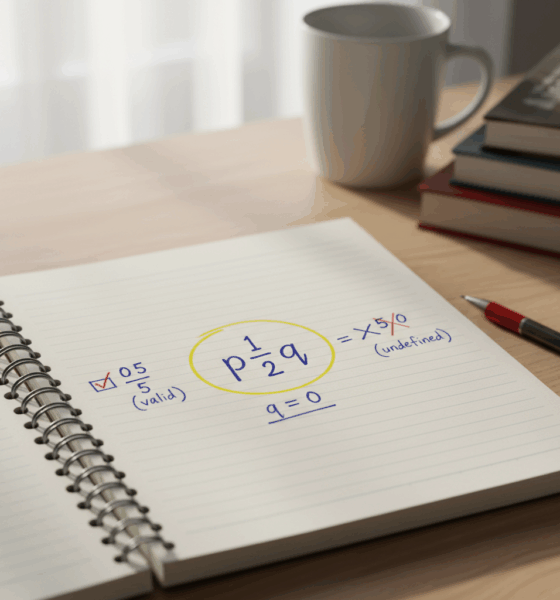
Технологии
ноль считается рациональным числом? объяснено просто
Рассматривается ли ноль рациональным числом? Простое объяснение, которое запоминается
Спросите любого ученика, который борется с дробями: является ли ноль рациональным числом? Чистый ответ в математике — да. Рациональным числом считается любое значение, которое можно записать в виде дроби p/q, где p и q — целые числа, а знаменатель q не равен нулю. Поскольку 0 можно представить как 0/1, 0/7 или, более общо, 0/n для любого ненулевого целого n, оно прекрасно подходит под определение. Но история становится богаче, если рассмотреть с точки зрения теории чисел, пределов и способов, которыми учащиеся усваивают математические понятия. Чтобы сделать материал более доступным, познакомьтесь с Майей, школьницей-программисткой, которая репетирует с младшими учениками; ей нравится простое объяснение, подкреплённое чёткими примерами и выявлением закономерностей.
Майя начинает с быстрого чек-листа. Если число имеет корректную дробную форму с целым числителем и ненулевым знаменателем, оно рационально. Ноль проходит тест, потому что его числитель может быть 0, а знаменатель — любым ненулевым целым числом. Деление на ноль запрещено, но это правило относится к знаменателю, а не к самому нулю. В классе такое разграничение предотвращает классическую путаницу: 0/5 корректно (и равно 0), тогда как 5/0 не определено. Эта одна фраза экономит часы недоразумений.
Для тех, кто любит контекст, ноль также входит в другие множества. Это целое число (…−2, −1, 0, 1, 2…), натуральное число (0, 1, 2, 3, …) и вещественное число (часть полного множества, включающего рациональные и иррациональные значения). Однако многие учебники определяют натуральные числа как начинающиеся с 1, исключая 0; в некоторых контекстах информатики 0 включается в натуральные числа. Знание используемой на курсе конвенции помогает избежать ненужных споров.
В классах 2025 года учителя всё чаще используют ИИ и объяснительные материалы, чтобы сделать эти различия запоминающимися. Инструменты для организации примеров — как проектные доски и планировщики контента — отражают аккуратность определения дробей. Для понимания, как структурированные инструменты мышления меняют учебные процессы, ресурсы по автоматизации с помощью API или обзор образовательных технологических трендов демонстрируют, как масштабируется ясность. Даже необычные исследования — например, что ощущается как миллиард секунд — помогают понять крупные и мелкие числа, встречающиеся в уроках по дробям и разрядам.
- ✅ Ноль рационален, потому что равен 0/n, где n ≠ 0.
- 🚫 Деление на ноль (например, 5/0) не определено и не связано с рациональностью нуля.
- 🧩 Ноль принадлежит нескольким множествам: целым, натуральным и вещественным числам.
- 🧠 Конвенции различаются для натуральных чисел; проверьте определение на вашем курсе.
- 🎯 Используйте тест дроби: целочисленный числитель и ненулевой знаменатель.
| Число 🔢 | Рационально? ✅/❌ | Причина 💡 |
|---|---|---|
| 0 | ✅ | Можно записать как 0/1, 0/5 … с целочисленными частями и ненулевым знаменателем. |
| 5 | ✅ | Равно 5/1 (форма целочисленной дроби). |
| 1/3 | ✅ | Целочисленный числитель и знаменатель; десятичная дробь периодическая. |
| π | ❌ | Нельзя выразить как отношение целых; десятичная дробь непериодическая. |
| √2 | ❌ | Доказано иррационально; нет целочисленной дроби, равной √2. |
Важное замечание: определение дроби само по себе определяет статус нуля — никаких споров, только структура.

Переход от дробной формы к реальному использованию нуля
Прежде чем перейти к свойствам, Майя задаёт практический вопрос: где ноль встречается вне тетрадей? В бюджетах строка с нулём означает отсутствие расходов; в коде 0 сигнализирует ложь или пустоту; в дашбордах 0 — это базовый уровень. Та же ясность, необходимая для признания 0 рациональным, помогает командам ярлычить, сравнивать и вычислять без неопределённостей. Для разработчиков, экспериментирующих с временными инструментами, понимание нуля как стартового смещения согласуется с надёжным инструментарием, например, точным получением времени в Swift для интервалов.
Почему 0 подходит под определение рационального числа: дроби, десятичные и алгебра
За формальным определением скрывается универсальность нуля как рационального числа, проявляющаяся во множестве представлений. В любой дроби p/q, если p = 0 и q ≠ 0, значение равно 0. Поэтому 0/1 = 0/9 = 0/−13 = 0. Изменение знаков или изменение знаменателя не меняет значение, поскольку умножение или деление нуля на любое ненулевое целое число всё равно даёт ноль. Это делает 0 самой устойчивой дробной величиной при эквивалентных преобразованиях.
Десятичные дроби рассказывают ту же историю. Рациональное число имеет конечное или периодическое десятичное представление. Десятичное представление нуля — 0.0, 0.000… или любая эквивалентная последовательность с конечным или бесконечным числом нулей — по сути, все варианты конечны. Если ученик видит 0.000, главное — нет ненулевых цифр после запятой; значит, число рационально и равно 0.
Алгебра усиливает понимание. Ноль — это аддитивный нейтралитет: для любого числа a, a + 0 = a. Это свойство гармонично сочетается с правилами рациональной арифметики. Например, прибавление 0 к рациональному числу p/q сохраняет рациональность p/q. Умножение любого рационала на 0 даёт 0, что опять же рационально. Замкнутость рациональных чисел и особая роль нуля взаимно дополняются: ничего не ломается, когда в компанию приходит ноль.
Майя демонстрирует классный прием, который учащиеся могут записать в конспекты или карточки. Прием избегает упрощений и выявляет важные правила.
- 🧪 Тест дроби: запишите число как p/q с целыми p, q и q ≠ 0 → рационально.
- 🔁 Тест десятичной дроби: конечная или периодическая → рационально (десятичная дробь нуля состоит из одних нулей).
- ➕ Проверка нейтрального элемента: прибавление 0 ничего не меняет; умножение на 0 даёт 0.
- 🧭 Знак: 0/−7 = 0/7 = 0; знак в знаменателе не влияет.
- ⚠️ Предупреждение: знаменатель 0 делает выражение неопределённым, а не «иррациональным».
| Представление 🧮 | Пример | Рационально? 🔍 | Обоснование 🧠 |
|---|---|---|---|
| Дробь | 0/19 | ✅ | Целочисленный числитель и ненулевой знаменатель → значение 0. |
| Десятичное | 0.000… | ✅ | Конечное (или фактически конечное) десятичное представление. |
| Целое число | 0 | ✅ | Любое целое число рационально (n = n/1). |
| Смешанное число | 0 0/5 | ✅ | Равно 0; дробная часть исчезает. |
| Научная нотация | 0.0 × 10³ | ✅ | По-прежнему 0; нотация не влияет на рациональность. |
Для любителей связей с технологиями помощники с ИИ могут помочь объяснениям оставаться последовательными; посмотрите, как коуч по письму для ясности или подобранные библиотеки для структурированных выводов отражают надёжность правил дробей. А если нужен прогресс за несколько недель, помощниками станут утилиты вроде календарных счётчиков.
Итог: независимо от того, записан ли ноль как дробь, десятичная дробь или целое число, он остаётся рациональным — и именно эта согласованность делает его таким полезным.
Распространённые заблуждения о нуле: деление, пределы и «сложные» случаи
Самая громкая путаница вокруг нуля возникает из-за смешения разных правил. Классическая ошибка — путать «деление на ноль не определено» и «ноль не рационален». Это не связано. В дроби p/q запрещено только q = 0. Установка p = 0 разрешена и безвредна. Майя приводит простую аналогию: знаменатель, равный нулю, — как запросить место в рейсе, которого нет — никакой посадочный талон не поможет. Но числитель, равный нулю, значит просто, что пассажиров нет; рейс всё равно существует.
Пределы создают следующий узел. Рассмотрим lim (x→0) 1/x. Подход справа движется к +∞; слева — к −∞. Это говорит о поведении рядом с нулём, а не о значении самого нуля или его рациональности. Аналогично, «неопределённые формы» типа 0/0 появляются в исчислении при вычислении пределов, но выражение 0/0 как число не определено. Никакие эти аналитические идеи не отменяют членство нуля в рациональном множестве.
Другие сложные места появляются в комбинаторике и алгебре. Факториал 0! равен 1 по определению (что согласуется с рекурсией и пустым произведением), и это рационально. Возведение в степень тоже может выглядеть странно: 0^0 в многих случаях осталось неопределённым, поскольку разные расширения противоречат желаемым свойствам; в дискретной математике иногда принимается равным 1 для упрощения формул. Хотя крайние правила есть, значение 0 остаётся рациональным.
- 🧯 Миф: «Деление на ноль доказывает, что 0 не рационален.» Реальность: знаменатель не может быть 0, числитель — может.
- 📉 Миф: «Пределы в 0 определяют, что такое ноль.» Реальность: пределы описывают поведение рядом, а не личность нуля.
- 🧩 Факт: 0! = 1 → рационально; 0^0 чувствителен к контексту, но не меняет рациональность нуля.
- 🔄 Факт: периодические десятичные дроби указывают на рациональность; десятичная дробь нуля — тривиальное повторение 0.
- 🧭 Совет: держите правила арифметики, теорему пределов и определения множеств в разных ментальных ящиках.
| Выражение/Идея 🧠 | Статус | Влияние на рациональность нуля 🎯 | Совет ученику ✍️ |
|---|---|---|---|
| 5/0 | Неопределено ❌ | Не влияет; не связано с тем, рационален ли 0. | Знаменатель не может быть 0. Точка. |
| 0/5 | Корректно ✅ | Подтверждает, что 0 — рациональное число. | Любой ненулевой знаменатель подходит. |
| lim (x→0) 1/x | Нет конечного предела | Не классифицирует 0; касается поведения рядом с ним. | Отделяйте исчисление от арифметики. |
| 0! | Равно 1 | Рационально (1/1) ✅ | Пустое произведение. |
| 0^0 | Зависит от контекста | Не меняет статус нуля | Следуйте правилам вашего курса. |
Когда ментальные модели требуют улучшения, помогают хорошо структурированные рабочие процессы. Статьи по улучшению дисциплины оценивания, например измерение важного в классах 2025 года, или по управлению сдвигами контекста, как в управлении контекстными окнами, показывают, как аккуратные определения предотвращают ошибки категоризации. Чёткие категории — вот что сохраняет ноль рациональным и запрещает деление на ноль — два факта, мирно сосуществующие рядом.

Связь с историей и аксиомами
Ученики часто спрашивают: если правила такие ясные, почему же человечество так долго не принимало ноль? Это отличный переход к истории о заполнительных знаках, торговцах и аксиомах, которые закрепили сегодняшние определения.
От древних заполнителей к современным аксиомам: как ноль заслужил своё место
Путь нуля от «ничего» до полноценного числа был далёк от мгновенного. Вавилонские писцы использовали символ-заполнитель для правильного позиционного значения, но концепция нуля как самостоятельного числа укоренилась в Индии, где математики, такие как Брахмагупта, сформулировали арифметику с нулём примерно в VII веке. Торговля и учёность распространили эти идеи через исламский мир в Европу, где сопротивление постепенно ослабело, когда позиционная запись показала свою незаменимость в торговле и астрономии. Возникновение алгебры, а затем исчисления закрепило центральную роль нуля.
Современные аксиоматические подходы делают классификацию безупречной. Начиная со структур вроде аксиом Пеано для натуральных чисел, математики конструируют целые числа из классов эквивалентности пар натуральных чисел, а рациональные — из классов эквивалентности пар целых (p, q) с q ≠ 0. В такой конструкции класс [(0, 1)] представляет рациональное число 0 — чётко и однозначно. Поэтому учебники уверенно утверждают, что ноль рационален. Единственное различие — включать ли ноль в натуральные числа; оба варианта согласованы, но преподаватели должны указывать эту конвенцию.
Майя использует короткую шкалу времени, чтобы помочь ученикам зафиксировать эволюцию. Это делает современное определение своего рода завершением долгого инженерного проекта: детали складываются, потому что их так задумали.
- 📜 Заполнители в древнем Вавилоне подготовили почву для позиционной записи.
- 🧮 Индийские математики формализовали арифметику с нулём и отрицательными числами.
- 🌍 Передача знаний через торговлю утвердила 0 в мировой математике.
- 🏛️ Аксиоматические конструкции вывели рациональные числа из целых с q ≠ 0.
- 🔧 Вычисления и наука о данных стандартизировали роль нуля в индексах и логике.
| Эпоха ⏳ | Веха | Влияние на рациональность 0 🎯 | Запоминающий ход 📌 |
|---|---|---|---|
| Древняя | Появление заполнителя | Готовит позиционное мышление, но не число | «Пустое место» в числовой линии |
| Классическая Индия | 0 как число с операциями | Арифметические правила стабилизируются | 0 × a = 0, a + 0 = a |
| Средневековая передача | Торговля и учёность распространяют позиционную запись | Стандартизация записи | Торговцы нуждались в нулях |
| Современные аксиомы | Построение ℚ из целых через пары (p, q) | [(0, 1)] — рациональный 0 ✅ | q ≠ 0 — единственное ограничение |
Современные преподаватели часто сочетают исторический контекст с цифровыми инструментами для лучшего запоминания. Блоги класса, раскрывающие спорные технологические истории — например, юридические споры с ИИ — показывают, как важны точные определения. Аналогично, статьи, сравнивающие помощников, такие как Copilot vs. ChatGPT, повторяют идею, что последовательные правила ведут к доверительным результатам. Даже обсуждения обращения с данными и анализа файлов закрепляют урок: чистые вводы и чёткие ограничения — как q ≠ 0 — удерживают системы в стабильности.
Вывод для учеников: ноль не появился просто так; он был инженерно встроен в числовую систему, и его рациональность заложена конструктивно.
Практическое мышление: быстрый классификатор чисел (с нулём в качестве опоры)
Когда большая картина ясна, Майя проводит «90-секундный сортировщик» для задач. Идея — быстро классифицировать любой ввод, проверяя дробную форму, поведение десятичных и принадлежность множествам — используя ноль как образец. Цель — скорость без ошибок. Ученики могут даже сделать мини-шпаргалку для полей тестов.
Начните с теста дроби. Можно ли записать как p/q с целыми p, q и q ≠ 0? Если да — рационально. Если десятичная форма конечная или периодическая (например, 0.125 или 0.333…), — рационально. Если ни то ни другое (например, π или √2 в виде десятичных), — иррационально. Для целых чисел помните, что n = n/1, значит каждое целое рационально; значит 0 рационален, так как 0 = 0/1. Эти проверки применимы повсеместно.
- 🧩 Шаг 1: Попробуйте записать как p/q с целыми; сразу отвергайте q = 0.
- 🔎 Шаг 2: Проверьте десятичные: конечные или периодические → рациональные.
- 🧱 Шаг 3: Целые автоматически подходят (n = n/1), включая 0.
- 🛑 Шаг 4: Если ничего не подходит и десятичные не периодические → иррационально.
- 🗂️ Шаг 5: Отметьте принадлежность к множествам (целые, натуральные, вещественные) для полного балла.
| Значение 🔢 | Дробная форма | Рационально? ✅/❌ | Метки множеств 🏷️ |
|---|---|---|---|
| 0 | 0/1 | ✅ | Целое, Натуральное, Вещественное |
| −3/4 | −3/4 | ✅ | Рациональное, Вещественное |
| 0.125 | 1/8 | ✅ | Рациональное, Вещественное |
| 0.333… | 1/3 | ✅ | Рациональное, Вещественное |
| √2 | — | ❌ | Иррациональное, Вещественное |
| π | — | ❌ | Иррациональное, Вещественное |
Хотите аудиовизуальное подкрепление? Быстрый объяснительный видеоролик помогает закрепить границу между рациональными и иррациональными, при этом сохраняя ноль в центре внимания. Учителям, формирующим плейлисты, структурированные запросы помогут находить лаконичные клипы.
Технически ориентированные ученики часто создают прототипы систем заметок и рабочих потоков; если это ваш стиль, модульные процессы, такие как виртуализированные медиа-серверы, могут хранить учебные материалы, а автоматизация задач через API-инструменты могут автоматически генерировать обучающие карточки для сложных граничных случаев, таких как 0, 0/0 (неопределено) и 1/0 (неопределено). Чистый рабочий процесс усиливает четкие определения.
Заключительная мысль для этого раздела: последовательность побеждает. Ноль ведёт себя одинаково во всех представлениях, делая его идеальной опорой для классификатора.
Крайние применения: разряды, информационные системы и учебные истории, где важен ноль
Рациональность нуля — это не просто доказательство; она лежит в основе того, как работают информационные системы и учебные программы. В десятичной системе разрядов цифра 0 сигнализирует «отсутствие этой позиции», что сохраняет правильность величины: 101 отличается от 11, потому что средний 0 сохраняет разряд десятков пустым. В таблицах и коде ноль часто обозначает «нет элементов», «нет ошибки» или базовую линию — делая вычисления предсказуемыми. Некорректное обращение с 0 вызвало бы хаос в дашбордах, вычислениях времени и алгоритмах.
Рассмотрите задачи классификации данных: если колонка должна хранить только рациональные числа, ноль должен быть допущен, иначе допустимые данные на базовом уровне будут отвергнуты. Майя создаёт небольшой демо-тест «гигиены данных»: парсер принимает микс из целых чисел, простых дробей, периодических десятичных и известных иррациональных; валидатор принимает всё, что конвертируется в p/q с q ≠ 0. Демо фиксирует 0 как валидное значение как в целочисленной, так и в дробной ветке. Далее ученики пишут модульные тесты, подтверждающие замкнутость при сложении и умножении с нулём.
- 🧮 Разряды: 0 сохраняет правильное выравнивание цифр, предотвращая ошибки при вычислении величины.
- 🧰 Целостность данных: ноль должен валидироваться в полях с рациональными числами.
- 🧷 Обработка ошибок: ошибки 1/0 фиксируются при парсинге, а не во время выполнения.
- 🧪 Тестирование: включайте 0 во все тесты замкнутости для рациональных чисел.
- 📚 Учебный сценарий: Майя обозначает 0 как «якорь» в рубриках и проектах.
| Сценарий 🗂️ | Роль нуля | Почему помогает рациональность 🎓 | Сигнал в классе 🛎️ |
|---|---|---|---|
| Разряды | Держит пустые позиции | Обеспечивает согласованное понимание величины | «0 сохраняет место» 😊 |
| Валидация | Принимается как 0/1 | Чёткие ограничения на ввод | Тестируйте 0, 1/0, 0/0 отдельно |
| Вычисления | Аддитивный нейтралитет | Упрощает доказательства и код | Используйте 0 в модульных тестах |
| Обучение | Опорный case | Снижает распространение заблуждений | Начинайте с 0 |
Пауза для любопытства: общение вокруг математики выигрывает от точного языка и контекста. Даже вне математики важна ясность — будь то анализ значений эмодзи для тона в студенческих форумах, оценка технологий безопасности в школах или распознавание новостных нарративов. Урок переноса: определения, ограничения и примеры предотвращают путаницу. В то же время безобидное увлечение, как толкование символов, напоминает учащимся, насколько быстро может смещаться смысл без общих правил — именно поэтому рациональное определение закрепляет ноль на месте.
Заключительный вывод для этого сегмента: рациональность нуля — это больше, чем ярлык; это гарантия того, что системы — от арифметики до аналитики — остаются предсказуемыми.
Дополнительная практика с мини-набором Майи
Ученики Майи классифицируют следующие числа за минуту: 0, −7, 2/9, 0/3, 3/0, 0.1010010001…, и √9. Результаты: 0 (рационально), −7 (рационально), 2/9 (рационально), 0/3 (рационально), 3/0 (неопределено), 0.1010010001… (непериодическая, непредельная → скорее всего иррациональная), √9 (равно 3 → рационально). Навыки выявления закономерностей переходят между разделами и тестами.
{“@context”:”https://schema.org”,”@type”:”FAQPage”,”mainEntity”:[{“@type”:”Question”,”name”:”Рассматривается ли ноль рациональным числом?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Да. По определению, рациональное число — любое значение, выражаемое как p/q с целыми p и q и q ≠ 0. Ноль подходит, потому что 0 = 0/1, 0/5 или 0/n для любого ненулевого целого n.”}},{“@type”:”Question”,”name”:”Деление на ноль делает ноль нерациональным?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Нет. Деление на ноль — это правило про знаменатели, а не про само число ноль. Выражения 5/0 и 0/0 не определены, но сам ноль остаётся допустимым рациональным числом.”}},{“@type”:”Question”,”name”:”Является ли ноль целым, натуральным или полным числом?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Ноль — целое и полное число. Относительно натуральных чисел — зависит от конвенции: во многих курсах натуральные числа начинаются с 1, но в некоторых контекстах ноль включается.”}},{“@type”:”Question”,”name”:”Можно ли записать ноль в десятичной форме и при этом он останется рациональным?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Да. Десятичное представление нуля — 0.0 (или 0.000…), оно конечное. По определению, числа с конечной или периодической десятичной формой рациональны.”}},{“@type”:”Question”,”name”:”Какова роль нуля в алгебре?”,”acceptedAnswer”:{“@type”:”Answer”,”text”:”Ноль — аддитивный нейтралитет: a + 0 = a. Он сохраняет уравнения сбалансированными и упрощает доказательства. Умножение любого рационального числа на 0 даёт 0, что рационально.”}}]}Рассматривается ли ноль рациональным числом?
Да. По определению, рациональное число — любое значение, выражаемое как p/q с целыми p и q и q ≠ 0. Ноль подходит, потому что 0 = 0/1, 0/5 или 0/n для любого ненулевого целого n.
Деление на ноль делает ноль нерациональным?
Нет. Деление на ноль — это правило про знаменатели, а не про само число ноль. Выражения 5/0 и 0/0 не определены, но сам ноль остаётся допустимым рациональным числом.
Является ли ноль целым, натуральным или полным числом?
Ноль — целое и полное число. Относительно натуральных чисел — зависит от конвенции: во многих курсах натуральные числа начинаются с 1, но в некоторых контекстах ноль включается.
Можно ли записать ноль в десятичной форме и при этом он останется рациональным?
Да. Десятичное представление нуля — 0.0 (или 0.000…), оно конечное. По определению, числа с конечной или периодической десятичной формой рациональны.
Какова роль нуля в алгебре?
Ноль — аддитивный нейтралитет: a + 0 = a. Он сохраняет уравнения сбалансированными и упрощает доказательства. Умножение любого рационального числа на 0 даёт 0, что рационально.

-

 Модели ИИ2 days ago
Модели ИИ2 days agoКак выбрать оптимальный ИИ для написания эссе в 2025 году
-

 Технологии1 day ago
Технологии1 day agoВаша карта не поддерживает этот тип покупки: что это значит и как решить проблему
-

 Модели ИИ1 day ago
Модели ИИ1 day agoOpenAI vs Tsinghua: Выбор между ChatGPT и ChatGLM для ваших AI-потребностей в 2025 году
-
 Модели ИИ23 hours ago
Модели ИИ23 hours agoOpenAI против Jasper AI: какой инструмент ИИ поднимет ваш контент в 2025 году?
-

 Интернет23 hours ago
Интернет23 hours agoИзучение будущего: что вам нужно знать о ChatGPT с поддержкой интернета в 2025 году
-

 Модели ИИ1 day ago
Модели ИИ1 day agoВыбор вашего AI-исследовательского помощника в 2025 году: OpenAI vs. Phind